Д'АЛАМБЕРА ПРИЗНАК

Д'АЛАМБЕРА ПРИЗНАК сходимости ряда: если для числового ряда

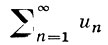
существует такое число q, 0 < q < 1, что начиная с нек-рого номера выполняется неравенство

|u_n+1/u_n| < q,

то данный ряд абсолютно сходится; если же начиная с нек-рого номера

|u_n+1/u_n| ≥ 1,

то ряд расходится. В частности, если существует предел

lim_n→∞ |u_n+1/u_n| < 1,

то рассматриваемый ряд абсолютно сходится, а если

lim_n→∞ |u_n+1/u_n| > 1,

то он расходится. Напр., ряд

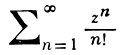
абсолютно сходится для всех комплексных z, так как

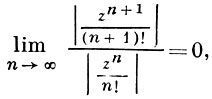
а ряд 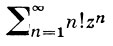расходится при всех z ≠ 0, так как

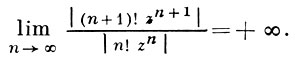
Если

lim_n→∞ |u_n+1/u_n| = 1,

то ряд может как сходиться, так и расходиться: ряды

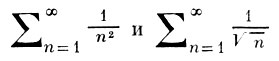
удовлетворяют этому условию, причем первый ряд сходится, а второй расходится.

Установлен Ж. Д'Аламбером (J. D'Alembert, 1768).

Л. Д. Кудрявцев.

Источники:

1. Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.