ГРУППОВОЙ ОБЪЕКТ

ГРУППОВОЙ ОБЪЕКТ категории - объект X категории С такой, что для любого Y ∈ Оb(С) множество морфизмов Ноm_C(Y, Х) является группой, а соответствие Y → Ноm_C(Y, X) - функтором из категории С в категорию групп (Gr). Гомоморфизмом Г. о. X в Г. о. Y наз. такой морфизм f : Х → Х' категории С, что для любого Y ∈ Оb(С) соответствующее отображение Ноm_C(Y, Х) → Ноm_C(Y, X') является гомоморфизмом групп. Г.о. категории С образуют подкатегорию (Gr - С) категории С; морфизмами в этой категории служат гомоморфизмы. Функтор X → h_X = Hom_C(⋅, X) устанавливает эквивалентность категории (Gr - С) и категории представимых предпучков групп на категории С. В случае, когда значения функтора h_X : Y → Ноm_C(Y, X) принадлежат подкатегории (Ab) абелевых групп, Г. о. X наз. коммутативным, или абелевым. Если категория С обладает конечными произведениями и финальным объектом е, то Г. о. X категории С определяются следующими свойствами.

Существуют морфизмы m: Х × Х → Х (умножение), r : Х → Х (обращение) и β : е → Х (единица), к-рые удовлетворяют следующим аксиомам.

а) Ассоциативность. Диаграмма

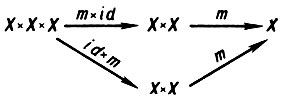
коммутативна.

б) Существование единичного элемента. Диаграмма

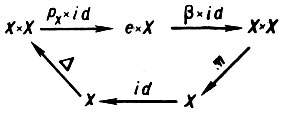
коммутативна.

в) Существование обратного элемента. Диаграмма

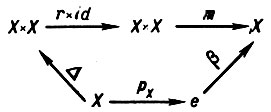
коммутативна. Здесь всюду р_X: Х → е - канонический морфизм объекта X в финальный объект е, а Δ : Х → Х × Х - диагональный морфизм.

В случае, когда С есть категория множеств (Ens), Г. о. X суть в точности группы. Финальным объектом категории (Ens) является множество {е}, состоящее из одного элемента е. Аксиома а) означает ассоциативность бинарной операции, задаваемой морфизмом m : X × X → X. Морфизм r : Х → Х есть отображение обращения, а морфизм β : {е} → Х есть отображение множества {е} в X, образ к-рого равен единичному элементу в X.

Аналогичным способом можно определить кольцевой объект категории и вообще задать алгебраическую структуру на объекте категории (см. [2]).

Лит.: [1] Мании Ю. И., «Успехи матем. наук», 1963, т. 18, в. 6; [2] Demazure М., Grothendieck А., Schemas en groupes, t. 1, В.-Hdlb.-N.Y., 1970.

И. В. Долгачев.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.