ГРУППОВОЕ ИСЧИСЛЕНИЕ

ГРУППОВОЕ ИСЧИСЛЕНИЕ - ассоциативное исчисление, в к-ром эффективным образом выполнено естественное групповое требование существования обратной операции. Именно, ассоциативное исчисление 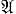наз. Г. и. (см. [1], с. 341), если для него может быть построен инвертирующий алгоритм, т. е. такой алгоритм 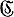, что для всякого слова Р в алфавите А исчисления 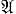выполняются следующие условия:

1) 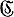(Р) определено и также является словом в А;

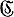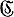2) слова Р(Р) и (Р)Р эквивалентны в 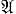пустому слову (алгоритм здесь следует понимать в к.-л. точном смысле слова, напр. как нормальный алгорифм).

Наиболее употребительными являются Г. и. специального типа (так наз. инверсивные исчисления, см. [2]), у к-рых существование инвертирующего алгоритма обеспечивается надлежащим подбором их алфавитов и списков соотношений: алфавит инверсивного исчисления имеет четную длину, для каждой его буквы ξ явно, указывается обратная ей буква ξ^-1, а в список соотношений включается полный набор так наз. тривиальных соотношений, т. е. соотношений, правые части к-рых суть пустые слова, а левые имеют вид ξξ^-1.

Роль Г. и. определяется тем, что они являются представлениями конечно определенных групп. Г. и. 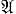, как и всякое ассоциативное исчисление, стандартным образом (см. Ассоциативное исчисление) порождает конечно определенную ассоциативную систему К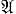, к-рая вследствие наличия у 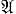инвертирующего алгоритма оказывается группой. Алгоритмическая проблема распознавания эквивалентности слов в Г. и. 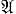представляет собой формулированную в терминах Г. и. проблему тождества для конечно определенной группы K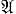. Это - первая из числа фундаментальных проблем разрешимости, сформулированных в 1911 М. Деном [3] для конечно определенных групп. Рядом авторов было найдено положительное решение этой проблемы для групп, определяемых частными типами Г. и. В частности, оно было получено для групп, определяемых инверсивными исчислениями с одним нетривиальным соотношением (см. [4]). В 1952 П. С. Новиков (см. [5], а также [6]) впервые построил пример конечно определенной группы с неразрешимой проблемой тождества, т. е. группы, порожденной таким Г. и., для к-рого невозможен никакой алгоритм в уточненном смысле слова (напр., Тьюринга машина или нормальный алгорифм), решающий проблему эквивалентности слов в этом Г. и. Этот пример дает отрицательное решение проблемы тождества для конкретной конечно определенной группы с учетом современного уточнения этой проблемы, даваемого теорией алгоритмов (см. Чёрча тезис). Впоследствии были приведены др. примеры таких Г. и. (см., напр., [7], [8]).

Упомянутый пример П. С. Новикова дает отрицательное решение и второй фундаментальной проблемы Дэна - проблемы распознавания пар слов, сопряженных в данном Г. и. Позднее П. С. Новиков [9] дал более простое и независимое от указанного примера отрицательное решение проблемы сопряженности.

Большой интерес с алгебраич. точки зрения представляет изучение тех свойств Г. и., к-рые оказываются инвариантными относительно изоморфизмов Г. и.,- это свойства абстрактных конечно определенных групп. В 1955 С. И. Адян [10]-[12] получил весьма общий результат, аналогичный результату А. А. Маркова для ассоциативных исчислений, давший отрицательное решение практически всех известных в то время алгоритмич. проблем, связанных с основными классификациями Г. и. В. частности, им было получено отрицательное решение третьей проблемы Дена - проблемы изоморфии любой фиксированной конечно определенной группе. Впоследствии аналогичные результаты получил М. Рабин [13].

Неразрешимость упомянутых алгоритмич. проблем, касающихся Г. и., повлекла за собой отрицательное решение ряда алгоритмич. проблем топологии. Так, по Г. и. с неразрешимой проблемой сопряженности можно построить двумерный полиэдр, для к-рого неразрешима проблема гомотопии путей. Опираясь на результаты С. И. Адяна, А. А. Марков получил в 1958 отрицательное решение проблемы гомеоморфии (см. [14]).

Лит.: [1] Марков А. А., Теория алгорифмов, М., 1954; [2] его же, «Изв. АН СССР. Сер. матем.», 1963, т. 27, №4, с. 907-36; [3] Dehn М., «Math. Ann.», 1911, Bd 71, S. 116; [4] Magnus W., «J. reine und angew. Math.», 1931, Bd 163, № 2, S. 141-65; [5] Новиков П. С., «Докл. АН СССР», 1952, т. 85, с. 709-12; [6] его же, Об алгоритмической неразрешимости проблемы тождества слов в теории групп М., 1955; [7] Boone W. W., «Indagat. math.», 1954, v. 16, p. 231, 492; 1955, v. 17, p. 252-56; 1957, v. 19, p. 22-7, 227-32; [8] BrittonJ. L., «Рrос. London Math. Soc.», 3 ser., 1958,' v. 8, № 32, p. 493-506; [9] Hовиков П. С., «Изв. АН СССР. Сер. матем.», 1954, т. 18, №6, с. 485-524; [10] Адян С. И., «Докл. АН СССР», 1955, т. 103, с. 533-35; [11] его же, там же, 1957, т. 117, № 1,с. 9-12; [12] его же, «Тр. Моск. матем. об-ва», 1957, т. 6, с. 231-98; [13] Rabin М. О., «Аnn. Math.», 1958, v. 67, p. 172-94; [14] Марков А. А., «Докл. АН СССР», 1958, т. 121, № 2, с. 218-20.

Н. М. Нагорный.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.