
ГРУПП МНОГООБРАЗИЕ
ГРУПП МНОГООБРАЗИЕ - класс всех групп, удовлетворяющих фиксированной системе тождественных соотношений
v(x1, ..., xn) = 1,
где v пробегает нек-рое множество V групповых слов, т. е. элементов свободной группы X со свободными образующими x1, ..., xn, ... . Как и всякое алгебраических систем многообразие Г. м. может быть определено также замкнутостью относительно подсистем (подгрупп), гомоморфных образов и декартовых произведений. Наименьшее многообразие, содержащее данный класс 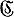 групп, обозначается var
групп, обозначается var 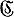 . Относительно операций пересечения многообразий и объединения многообразий, определяемого формулой
. Относительно операций пересечения многообразий и объединения многообразий, определяемого формулой
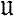 ∨ ℬ = var (
∨ ℬ = var (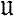 ∪ ℬ),
∪ ℬ),
Г. м. образуют полную модулярную, но не дистрибутивную решетку. Произведение 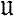 ℬ многообразий
ℬ многообразий 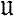 и ℬ определяется как Г. м., состоящее из всех групп G, обладающих нормальной подгруппой N ∈
и ℬ определяется как Г. м., состоящее из всех групп G, обладающих нормальной подгруппой N ∈ 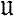 такой, что G/N ∈ ℬ. Каждое Г. м., отличное от многообразия единичных групп и многообразия всех групп, однозначно представимо в виде произведения далее неразложимых Г. м.
такой, что G/N ∈ ℬ. Каждое Г. м., отличное от многообразия единичных групп и многообразия всех групп, однозначно представимо в виде произведения далее неразложимых Г. м.
Примеры Г. м.: многообразие 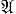 всех абелевых групп, бернсайдово многообразие ℬ всех групп экспоненты (показателя) n, определяемое тождеством хn = 1, многообразие
всех абелевых групп, бернсайдово многообразие ℬ всех групп экспоненты (показателя) n, определяемое тождеством хn = 1, многообразие 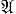 n = ℬn ∧
n = ℬn ∧ 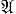 , многообразие
, многообразие 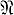 c всех нильпотентных групп класса ≤ с, многообразие
c всех нильпотентных групп класса ≤ с, многообразие 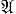 l всех разрешимых групп длины ≤l, в частности при l = 2,
l всех разрешимых групп длины ≤l, в частности при l = 2, 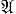 3 - многообразие метабелевых групп.
3 - многообразие метабелевых групп.
Пусть 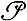 - нек-рое свойство групп. Говорят, что Г. м. ℬ обладает свойством
- нек-рое свойство групп. Говорят, что Г. м. ℬ обладает свойством 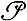 (локально обладает свойством
(локально обладает свойством 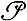 ), если каждая группа из ℬ (каждая конечно порожденная группа из ℬ) обладает свойством
), если каждая группа из ℬ (каждая конечно порожденная группа из ℬ) обладает свойством 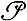 . Именно в этом смысле говорят, что многообразие нильпотентное, локально нильпотентное, локально конечное и т. д.
. Именно в этом смысле говорят, что многообразие нильпотентное, локально нильпотентное, локально конечное и т. д.
Свойства разрешимого Г. м. ℬ зависят от 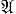 . Так, если ℬ ⊉
. Так, если ℬ ⊉ 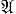 2, то ℬ ⊆ ℬn
2, то ℬ ⊆ ℬn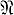 cℬn при нек-рых подходящих n и с (см. [2], [3]). Описание метабелевых Г. м. в значительной степени сводится к описанию локально конечных Г. м.: если метабелево многообразие ℬ не локально конечно, то
cℬn при нек-рых подходящих n и с (см. [2], [3]). Описание метабелевых Г. м. в значительной степени сводится к описанию локально конечных Г. м.: если метабелево многообразие ℬ не локально конечно, то
ℬ = ℬ1 ∨ ℬ2 ∨ ℬ3,
где ℬ1 = 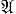 m
m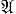 , ℬ2 однозначно представимо в виде объединения конечного числа Г. м. вида
, ℬ2 однозначно представимо в виде объединения конечного числа Г. м. вида 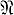 c
c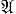 k ∧
k ∧ 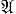 2, ℬ3, локально конечно [4]. Некоторые локально конечные метабелевые многообразия описаны, напр. многообразия р-групп класса ≤ р + 1 (см. [5]).
2, ℬ3, локально конечно [4]. Некоторые локально конечные метабелевые многообразия описаны, напр. многообразия р-групп класса ≤ р + 1 (см. [5]).
Г. м. наз. кроссовым, если оно порождается конечной группой. Кроссовы Г. м. локально конечны. Г. м. наз. почти кроссовым, если оно не кроссово, но всякое его собственное подмногообразие кроссово. Разрешимые почти кроссовы многообразия исчерпываются многообразиями 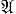 ,
, 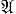 2p,
2p, 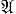 p
p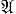 q
q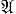 r,
r, 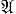 p
p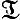 q, где p, q, r - различные простые числа,
q, где p, q, r - различные простые числа, 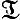 q = ℬq ∧
q = ℬq ∧ 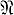 2 при нечетном q и
2 при нечетном q и 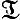 2 = ℬ4 ∧
2 = ℬ4 ∧ 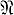 2 (см. [6]). Существуют, однако, другие почти кроссовы многообразия; такие, напр., содержатся во всяком многообразии
2 (см. [6]). Существуют, однако, другие почти кроссовы многообразия; такие, напр., содержатся во всяком многообразии 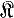 всех локально конечных групп экспоненты р ≥ 5 (см. [7]). В изучении локально конечных Г. м. важную роль играют критические группы - конечные группы, не лежащие в многообразии, порожденном всеми их собственными подгруппами и факторгруппами. В кроссовом многообразии может содержаться лишь конечное число неизоморфных критич. групп. Всякое локально конечное многообразие порождается своими критич. группами.
всех локально конечных групп экспоненты р ≥ 5 (см. [7]). В изучении локально конечных Г. м. важную роль играют критические группы - конечные группы, не лежащие в многообразии, порожденном всеми их собственными подгруппами и факторгруппами. В кроссовом многообразии может содержаться лишь конечное число неизоморфных критич. групп. Всякое локально конечное многообразие порождается своими критич. группами.
Г. м. наз. конечно базируемым, если оно может быть задано конечным числом тождеств. Таковы, напр., все кроссовы, нильпотентные и метабелевы многообразия. Доказано [8] существование не конечно базируемых Г. м. и континуальность количества всех Г. м. Примеры бесконечных независимых систем тождеств приведены в [9]. Произведение конечно базируемых Г. и. не обязано быть конечно базируемым, в частности ℬ4ℬ2 не имеет конечного базиса.
Г. м. наз. многообразием лиевского типа, если оно порождается своими нильпотентными группами без кручения. Если, кроме того, факторы нижнего центрального ряда свободных групп многообразия - группы без кручения, то многообразие наз. магнусовым. Класс многообразий лиевского типа не совпадает с классом магнусовых многообразий; каждый из них замкнут относительно операции умножения многообразий [10]. Магнусовыми являются, напр., многообразие всех групп, многообразия 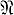 c,
c, 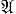 n и многообразия, получающиеся из многообразий
n и многообразия, получающиеся из многообразий 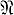 c с помощью применения в конечном числе операций пересечения и умножения [11].
c с помощью применения в конечном числе операций пересечения и умножения [11].
Лит.: [1] Нейман X., Многообразия групп, пер. с англ., М., 1969; [2] Каргаполов М. И., Чуркин В. А., «Алгебра и логика», 1971, т. 10, вып. 6, с. 651-57; [3] Groves J. R. F., «Bull. Austr. Math. Soc.», 1972, v. 7, № 3, p. 437-41; [4] Вrаусe R. A., «Philos. Trans. Roy. Soc. London», ser. A 266, 1970, № 1176, p. 281-355; [5] Brisley W., «J. Austr. Math. Soc.», 1971, v. 12, № 1, p. 53-63; [6] Ольшанский А. Ю., «Матем. сб.», 1971, т. 85, № 1, с. 115-31; [7] Размыслов Ю. П., «Алгебра и логика», 1971, т. 10, в. 1, с. 33-44; [8] Ольшанский А. Ю., «Изв. АН СССР. Сер. матем.», 1970, т. 34, № 2, с. 376-84; [9] Адян С. И., Проблема Бернсайда и тождества в группах, М., 1975; [10] Шмелькин А. Л., «Тр. Моск. матем. об-ва», 1973, т. 29, с. 247-60; [11] Горчаков Ю. М., «Сиб. матем. журнал», 1969, т. 10, № 5, С. 1023-33.
А. Л. Шмелькин.
Источники:
- Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'