ГРОТЕНДИКА КАТЕГОРИЯ

ГРОТЕНДИКА КАТЕГОРИЯ - абелева категория, обладающая семейством образующих и удовлетворяющая аксиоме: в категории 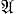существуют копроизведения (суммы) любых семейств объектов и для каждого направленного по возрастанию семейства подобъектов (U_i, μ_i], i ∈ I, и произвольного объекта А и каждого подобъекта (V, σ) выполнено равенство

(∪_i∈I (U_i, μ_i]) ∩ (V, σ] = ∪_i∈I(U_iμ_i] ∩ (V, σ]).

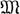Категория левых (правых) Λ-модулей над произвольным ассоциативным кольцом Λ с единицей и категории пучков Λ-модулей над произвольным топологич. пространством есть Г. к. Полная подкатегория категории _Λ левых Λ-модулей наз. подкатегорией локализации, если она замкнута относительно копределов и если в точной последовательности

0 → А' → A → А'' → 0,

объект А принадлежит тогда и только тогда, когда и А' и А'' принадлежат . Каждая подкатегория локализации позволяет построить факторкатегорию _Λ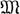/. Абелева категория тогда и только тогда является Г. к., когда она эквивалентна нек-рой факторкатегории вида _Λ/.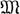

В Г. к. каждый объект обладает инъективной оболочкой, поэтому Г. к. хорошо приспособлены для гомологич. приложений.

Лит.: [1] Гротендик А., О некоторых вопросах гомологической алгебры, пер. с франц., М., 1961; [2] Букур И., Деляну А., Введение в теорию категорий и функторов, пер. с англ., М., 1972; [3] Popesсо N., Gabriel Р., «С. r. Acad. sci.», 1964, t. 258, № 17, p. 4188-90.

M. Ш. Цаленко.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.