ГРИНА ФУНКЦИЯ

ГРИНА ФУНКЦИЯ - функция, связанная с интегральным представлением решений краевых задач для дифференциальных уравнений.

Г. ф. краевой задачи для линейного дифференциального уравнения - фундаментальное решение уравнения, удовлетворяющее однородным краевым условиям. Г. ф. является ядром интегрального оператора, обратного к дифференциальному оператору, порожденному данным дифференциальным уравнением и однородными краевыми условиями. Г. ф. позволяет найти решения неоднородного уравнения, удовлетворяющие однородным краевым условиям. Нахождение Г. ф. сводит исследование свойств дифференциального оператора к изучению аналогичных свойств соответствующего интегрального оператора.

Функция Грина для обыкновенных дифференциальных уравнений.

Пусть L - дифференциальный оператор, порожденный дифференциальным полиномом

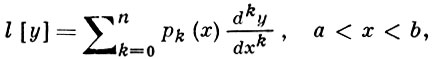
и краевыми условиями U_j[y] = 0, j = 1, 2, ..., n, где

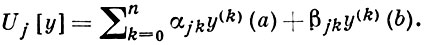
Г. ф. оператора L наз. функция G(x, ξ), удовлетворяющая условиям:

1) G(x, ξ) непрерывна и имеет непрерывные производные по х до (n - 2)-го порядка включительно для всех значений х и ξ из сегмента [а, b];

2) при любом фиксированном ξ из интервала (а, b) функция G(x, ξ) имеет равномерно непрерывные производные n-го порядка по х в каждом из полусегментов [а, ξ) и (ξ, b], причем производная (n - 1)-го порядка при х = ξ удовлетворяет условию

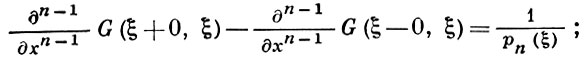
3) в каждом из полусегментов [а, ξ) и (ξ, b] функция G(x, ξ), рассматриваемая как функция от х, удовлетворяет уравнению l_x[G] = 0 и краевым условиям U_jx[G] = 0, j = 1, 2, ..., n.

Если краевая задача Ly = 0 имеет лишь тривиальные решения, то оператор L имеет и притом только одну Г. ф. (см. [1]). При этом для любой функции f(x), непрерывной на сегменте [а, b], существует решение краевой задачи Ly = f, и это решение задается формулой

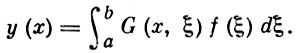
Если оператор L имеет Г. ф. G(x, ξ), то сопряженный оператор L* также имеет Г. ф., к-рая равна G̅(ξ, х). Если, в частности, оператор L самосопряженный (L = L*), то G(x, ξ) = G̅(ξ, х), то есть Г. ф. в этом случае является эрмитовым ядром. Напр., Г. ф. самосопряженного оператора L 2-го порядка, порожденного дифференциальной операцией с действительными коэффициентами

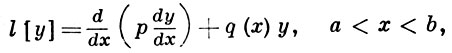
и краевыми условиями y(a) = 0, у(b) = 0, имеет вид:

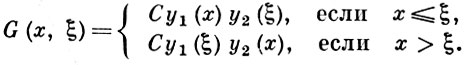
Здесь y₁(x) и у₂(х) - произвольные решения уравнения l[у] = 0, удовлетворяющие соответственно условиям y₁(а) = 0, y₂(b) = 0; C = [p(ξ) W(ξ))^-1, где W - определитель Вронского {вронскиан) решений y₁ и у₂, причем можно показать, что С не зависит от ξ.

Если оператор L имеет Г. ф., то краевая задача на собственные значения Lу = λу эквивалентна интегральному уравнению

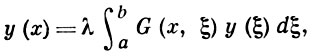
к которому применима теория Фредгольма. Поэтому краевая задача Lу = λу может иметь не более счетного числа собственных значений λ₁, λ₂, ..., у которых отсутствуют конечные предельные точки. Сопряженная задача имеет комплексно сопряженные собственные значения той же кратности. Для каждого λ, не являющегося собственным значением оператора L, можно построить Г. ф. G(x, ξ, λ) оператора L - λI, где I - тождественный оператор. Функция G₁(x, ξ, λ) является мероморфной функцией параметра λ; ее полюсами могут быть лишь собственные значения оператора L. Если кратность собственного значения λ₀ равна единице, то

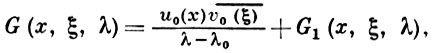
где G(x, ξ, λ) регулярна в окрестности точки λ, а u₀(х) и v₀(x) - собственные функции операторов L и L*, отвечающие собственным значениям λ₀ и λ̅₀ и нормированные так, что

Если G(x, ξ, λ) имеет бесконечно много полюсов и при том только 1-го порядка, то существует полная биортогональная система

u₁(х), u₂(х), ...; v₀(x), v₂(x), ...

собственных функций операторов L и L*. Если занумеровать собственные значения в порядке возрастания их абсолютных величин, то интеграл

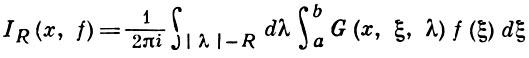
равен частичной сумме

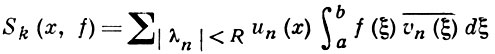
разложения функции f по собственным функциям оператора L. Положительное число R выбирается так, чтобы на окружности |λ| = R функция G(x, ξ, λ) была регулярной по λ. Для регулярной краевой задачи и для любой кусочно гладкой функции f(x) в интервале а < х < b выполняется равенство

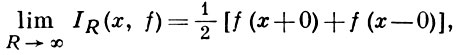
т. е. имеет место разложимость в сходящийся ряд (см. [1]).

Если Г. ф. G(x, ξ, λ) оператора L - λI имеет кратные полюсы, то ее главная часть выражается через канонич. системы собственных и присоединенных функций операторов L и L* (см. [2]).

Выше рассматривался случай, когда краевая задача Ly = 0 не имела нетривиальных решений. Если же эта краевая задача имеет нетривиальные решения, то вводят так наз. обобщенную Грина функцию. Пусть, напр., имеется ровно m линейно независимых решений задачи Ly = 0. Тогда существует обобщенная Г. ф. G̃(x, ξ), к-рая обладает свойствами 1) и 2) обычной Г. ф., при а < ξ < b удовлетворяет как функция х краевым условиям и, кроме того, является решением уравнения

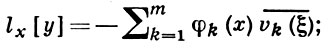
здесь {v_k(x)}^m_k=1 - система линейно независимых решений сопряженной задачи L*y = 0, а {φ_k(x)}^m_k=1 - произвольная биортогональная ей система непрерывных функций. Тогда

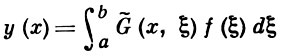
есть решение краевой задачи Ly = f, если функция f(x) непрерывна и удовлетворяет условию разрешимости, т. е. ортогональна всем v_k(x).

Если G̃₀(x, ξ) - одна из обобщенных Г. ф. оператора L, то любая другая обобщенная Г. ф. может быть представлена в виде

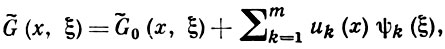
где {u_k(х)} - полная система линейно независимых решений задачи Ly = 0, а ψ_k(ξ) - произвольные непрерывные функции (см. [3]).

Функция Грина для дифференциальных уравнений с частными производными. 1) Эллиптические уравнения. Пусть А - эллиптический дифференциальный оператор порядка m, порожденный дифференциальным полиномом

а(х, D) = ∑_|α|≤m a_α(x) D^α

в ограниченной области Ω ⊂ R^N и однородными краевыми условиями B_ju = 0, где B_j - граничные операторы с коэффициентами, определенными на границе ∂Ω области Ω, к-рая предполагается достаточно гладкой. Функция G(x, у) наз. Г. ф. оператора А, если при любом у ∈ Ω она удовлетворяет однородным краевым условиям B_jxG(x, у) = 0 и, рассматриваемая как обобщенная функция, удовлетворяет уравнению

а(х, D) G(x, у) = δ(х - у).

В случае операторов с гладкими коэффициентами и нормальных граничных условий, обеспечивающих единственность решения однородной краевой задачи, Г. ф. существует и решение краевой задачи Au = f представляется в виде (см. [4])

u(x) = ∫_Ω G(x, y)f(y)dy.

В этом случае для Г. ф. справедливы равномерные при x ∈ Ω̅, y ∈ Ω̅ оценки

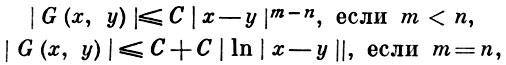
и Г. ф. равномерно ограничена, если m > n.

Краевая задача на собственные значения Аu = λu эквивалентна интегральному уравнению

u(x) = λ ∫_Ω G(х, у) u(у) dy,

для к-рого применима теория Фредгольма (см. [5]). При этом Г. ф. сопряженной краевой задачи равна G̅(y, х). Отсюда, в частности, следует, что может существовать не более чем счетное число собственных значений и что они не имеют конечных предельных точек, а сопряженная краевая задача имеет комплексно сопряженные собственные значения той же кратности.

Для уравнений 2-го порядка Г. ф. изучена полнее, поскольку явно выписывается вид особенности фундаментального решения. Так, для оператора Лапласа Г. ф. имеет вид

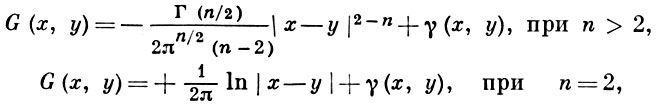
где γ(х, у) - гармоническая в области Ω функция, выбранная таким образом, чтобы Г. ф. удовлетворяла краевому условию.

Г. ф. G(x, у) первой краевой задачи для эллиптич. оператора 2-го порядка а(х, D) с гладкими коэффициентами в области Ω с границей ∂Ω типа Ляпунова позволяет выразить решение задачи

а(х, D) u(х) = f(х) при х ∈ Ω, u|_∂Ω = φ,

в виде

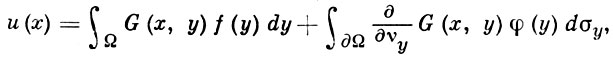
где ∂/∂ν_y - производная по внешней конормали для оператора а(х, D).

В случае, если однородная краевая задача Аu = 0 имеет нетривиальные решения, то, как и для обыкновенных дифференциальных уравнений, вводится обобщенная Г. ф. Так, напр., в случае второй краевой задачи для оператора Лапласа существует обобщенная Г. ф., наз. Неймана функцией (см. [3]).

2) Параболические уравнения. Пусть Р - параболический дифференциальный оператор порядка m, порожденный дифференциальным полиномом

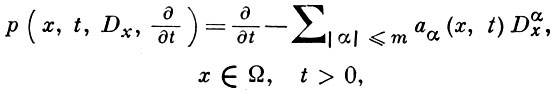
и однородными начальным и краевыми условиями

u(х, 0) = 0, B_ju(х, t) = 0,

где B_j - граничные операторы с коэффициентами, определенными при x ∈ ∂Ω и t ≥ 0. Г. ф. оператора Р наз. функция G(x, t, у, τ), к-рая для любых t > τ ≥ 0 и y ∈ Ω удовлетворяет по х однородным краевым условиям, является при (х, t) ≠ (y, τ) решением уравнения

p(x, t, D_x, ∂/∂t) G(х, t, у, τ) = 0

и для любой непрерывной функции φ(х) удовлетворяет соотношению

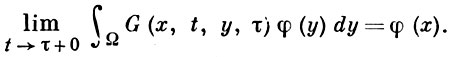
В случае операторов с гладкими коэффициентами и нормальных граничных условий, обеспечивающих единственность решения задачи рu = 0, Г. ф. существует, и решение уравнения

р(х, t, D_x, ∂/∂t) u(x, t) = f(x, t),

удовлетворяющее однородным краевым условиям и начальному условию u(х, 0) = φ(х), имеет вид

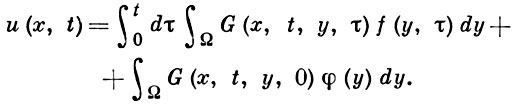
При изучении эллиптич. или параболич. систем вместо Г. ф. вводится понятие матрицы Грина, к-рая позволяет выразить решения однородных краевых задач для указанных систем в виде интегралов от произведений матрицы Грина на векторы правых частей и начальных условий (см. [7]).

Г. ф. наз. по имени Дж. Грина (G. Green), впервые рассмотревшего один ее частный случай в своем исследовании по теории потенциала (1828).

Лит.: [1] Наймарк М. А., Линейные дифференциальные операторы, 2 изд., М., 1969; [2] Келдыш М. В., «Докл. АН СССР», 1951, т. 77, № 1, с. 11 - 14; [3] Соболев С. Л., Уравнения математической физики, 4 изд., М., 1966; [4] Вере Л., Джон Ф., Шехтер М., Уравнения с частными производными, пер. с англ., М., 1966; [5] Garding L., «Math. scand.», 1953, v. 1, № 1, S. 55-72; [6] Фридман А., Уравнения с частными производными, параболического типа, пер. с англ., М., 1968; [7] Эйдельман С. Д., Параболические системы, М., 1964.

Ш. А. Алимов, В. А. Ильин.

Функция Грина в теории функций. В теории функций комплексного переменного под (действительной) Г. ф. понимается Г. ф. первой краевой задачи для оператора Лапласа, т. е. функция вида

(1)

где z = x + iy - комплексное переменное, z₀ = x₀ + iy₀ - полюс Г. ф., z₀ ∈ Ω, γ(z, z₀) - гармонич. функция z, принимающая на границе области ∂Ω значения - ln (1/|z - z₀|). Пусть область Ω односвязная и w = f(z, z₀) - аналитич. функция, реализующая конформное отображение области Ω на единичный круг в плоскости w так, что точка z₀ переходит в центр круга, f(z₀, z₀) = 0, f'(z₀, z₀) > 0.

Тогда

G(z, z₀) = ln (1/|f(z, z₀)|) (2)

Если H(z, z₀) - сопряженная гармоническая для G(z, z₀) функция, H(z₀, z₀) = 0, то аналитич. функция F(z, z₀) = G(z, z₀) + iH(z, z₀) наз. комплексной функцией Грина области Ω с полюсом z₀. Обращение формулы (2) дает

f(z, z₀) = e^{-F(z, z₀)} (3)

Формулы (2) и (3) показывают, что задачи построения конформного отображения области Ω на круг и отыскания Г. ф. эквивалентны. Г. ф. G(z, z₀), F(z, z₀) инвариантны относительно конформных отображений, что облегчает иногда их отыскание (см. Отображений метод).

В теории римановых поверхностей Г. ф. удобнее определить при помощи минимального свойства, справедливого для функции (1): среди всех положительных гармонияеских при z ≠ z₀ функций U(z, z₀) на римановой поверхности Ω, имеющих в окрестности точки z₀ вид

U(z, z₀) = ln (1/|z - z₀|) + γ(z, z₀). (4)

где γ(z, z₀) - регулярная на всей поверхности Q гармония, функция, Г. ф. G(z, z₀), если она существует, является наименьшей, т. е. G(z, z₀) ≤ U(z, z₀). При этом существование Г. ф. характерно для римановых поверхностей гиперболич. типа. Так определенная Г. ф. на (идеальной) границе римановой поверхности, вообще говоря, уже не везде обращается в нуль. Аналогично обстоит дело и в потенциала теории (см. также Потенциала теория абстрактная). Для произвольного открытого множества Ω, напр. в евклидовом пространстве ℝⁿ, n ≥ 2, Г. ф. G(x, х₀) также можно определить при помощи указанного минимального свойства, причем при n ≥ 3 в (4) вместо ln (1/|x - x₀|) следует писать |х - х₀|^2-n. Вообще говоря, при приближении к границе ∂Ω такая Г. ф. не обязательно стремится к нулю. Для римановых поверхностей параболич. типа и для нек-рых областей в ℝ² (напр., для Ω = ℝ²) Г. ф. не существует.

Лит.: [1] Стойлов С., Теория функций комплексного переменного, пер. с рум., т. 2, М., 1962; [2] Неванлинна Р., Униформизация, пер. с нем., М., 1955; [3] Брело М., Основы классической теории потенциала, пер. с франц., М., 1964.

Е. Д. Соломенцев.

Грина функция в статистической механике - упорядоченная по времени линейная комбинация корреляционных функций, удобная промежуточная величина при расчетах физич. характеристик систем большого числа взаимодействующих частиц.

1)Г. ф. в квантовой статистической механике. Наиболее часто применяются двувре-менные коммутаторные температурные Г. ф.: запаздывающие (ret, +), опережающие (adv, -) и причинные (с), определяемые соотношениями:

где

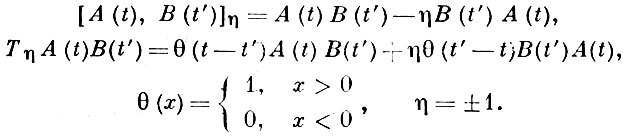
Здесь A(t) и B(t') - зависящие от времени динамич. величины (операторы в пространстве состояний системы в Гейзенберга представлении), через 〈...〉 обозначено среднее по Гиббса статистическому ансамблю; значение η = ±1 выбирается из соображений удобства. Эффективность применения Г. ф. в значительной степени обусловлена использованием спектральных представлений для их фурье-образов G⁽ⁿ⁾_AB(E), n = ret, adv, с. Так, напр., в случае ненулевой температуры для запаздывающих и опережающих Г. ф. справедливо представление:

Здесь J_AB(ω) - спектральная плотность; θ = kT, где Т - абсолютная температура, T ≠ 0, k - постоянная Больцмана; использована система единиц, в которой ħ = h/2π = 1, где h - постоянная Планка. Справедлива, в частности, формула:

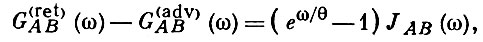
позволяющая вычислять спектральную плотность (а следовательно, и ряд физич. характеристик системы) через Г. ф. Аналогичные спектральные формулы существуют и для нуля температуры. Особенности (полюса на комплексной плоскости) фурье-образа Г. ф. характеризуют спектр и затухание элементарных возбуждений в системе. Основные источники вычисления Г. ф.: а) приближенное решение бесконечной цепочки зацепляющихся уравнений, к-рая выводится непосредственно из определения Г. ф. путем «расцепления» ее, исходя из тех или иных физич. соображений; б) суммирование «основных» с физич. точки зрения членов рядов теории возмущений (суммирование диаграмм); этот способ применяется в основном при вычислении причинных Г. ф. и имеет много общего с методикой расчета Г. ф. в квантовой теории поля.

2) Г. ф. в классической статистической механике. Вводятся опережающие (ret) и запаздывающие (adv) двувременные Г. ф. путем замены в соответствующих формулах для квантового случая (при η = +1) операторов A(t) и В(t') па функции динамич. состояния изучаемой классич. системы и коммутатора A(t)B(t') - B(t')A(t) (квантовые скобки Пуассона) - на классические (обычные) скобки Пуассона; соответственно под 〈...〉 понимается усреднение по классическому ансамблю Гиббса. Введение причинной Г. ф. здесь теряет смысл из-за коммутативности произведения динамич. величин. Аналогично квантовому случаю, существуют и могут быть эффективно использованы спектральные представления для фурье-образа Г. ф. Основным источником для вычисления классич. Г. ф. служат системы уравнений, получающиеся варьированием по бесконечно малому изменению гамильтониана той или иной системы уравнений для корреляционных функций: Боголюбова цепочки уравнений, системы уравнений гидродинамики и т. д.

Лит.: [1] Боголюбов Н. Н., Тябликов С. В., «Докл. АН СССР», 1959, т. 126, с. 53; [2] Зубарев Д. Н., «Успехи фнз. наук», 1960, т. 71, с. 71; [3] Боголюбов Н. Н. (мл.), Садовников Б. И., «Ж. эксперим. и теор. физ.», 1962, т. 43, в. 8, с. 677; [4] их же, Некоторые вопросы статистической механики, М., 1975; [5] Статистическая физика и квантовая теория поля, М., 1973.

В. Н. Плечко.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.