ГРЁТША ТЕОРЕМЫ

ГРЁТША ТЕОРЕМЫ - различные результаты о конформных и квазиконформных отображениях X. Грётша (см. [1]). На основе разработанного им полос метода, представляющего первую общую форму метода конформных модулей (см. Экстремальной метрики метод), X. Грётш систематически исследовал и решил большое количество экстремальных задач конформного отображения многосвязных (в том числе бесконечносвязных) областей, включая вопросы существования, единственности и геометрич. свойств экстремальных отображений. Ниже приведены нек-рые из простейших Г. т.

Среди всех однолистных конформных отображений w-f(z) фиксированного кругового кольца K_R = {z : R < |z| < 1}, при к-рых единичная окружность Г = {z: |z| = 1} переходит в себя, максимум диаметра образа окружности Г_R = {z : |z| = R } достигается в том и только в том случае, когда граничной компонентой f(Г_R) служит прямолинейный отрезок с серединой в точке w = 0. Аналогичный результат установлен для многосвязных областей.

Среди всех однолистных конформных отображений w = f(z) фиксированной многосвязной области B ∋ ∞ с разложением в бесконечности f(z) = z + O(1) (z → ∞) и с нормировкой f(z₀) = 0 в фиксированной точке z₀ ∈ B максимум |f'(z₀)|, максимум |f(z₁)| и минимум |f(z₁)| в фиксированной точке z₁ ∈ B, z₁ ≠ z₀, достигаются только на отображениях, переводящих каждую граничную компоненту В соответственно в дугу окружности с центром в точке w = 0; в дугу эллипса с фокусами в точках w = 0 и w = w' = f(z₁); в дугу гиперболы с фокусами в точках w = 0 и w = w'' = f(z₁). В каждой из указанных задач экстремальное отображение существует и единственно. В том же классе отображений для фиксированного z₁ ∈ B областью значений функционала Ф(f) = ln (f(z₁)/z₁) является круг

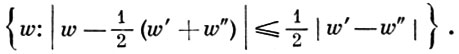
Каждая граничная точка этого круга является значением функционала Ф на единственном отображении из рассматриваемого класса, обладающем определенными геометрич. свойствами.

X. Грётш впервые предложил одну из форм представления квазиконформных отображений и перенес на эти отображения многие экстремальные результаты, установленные им ранее для конформных отображений.

Лит.: [1] Grötzsсh Н., «Веr. Verhandl. Sächsisch. Akad. Wiss. Leipzig. Math.-Naturwiss. Kl.», 1929, Bd 81, № 1, S. 38-47- №4, S. 217-21; 1930, Bd 82, №1, S. 69-80; 1932, Bd 84, № 4, S. 269-78; [2] Джeнкинс Дж., Однолистные Функции и конформные отображения, пер. с англ.. М., 1962.

П. М. Тамразов.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.