ГРЁТША ПРИНЦИП

ГРЁТША ПРИНЦИП - теорема в теории конформных отображений, предложенная в 1928 X. Грётшем [1] и используемая при доказательстве неравенств для длин кривых нек-рых семейств и площади занимаемой ими области; им же в дальнейшем были разработаны многочисленные применения развитого на этой основе полос метода в теории однолистных функций, заданных в конечносвязных или в бесконечносвязных областях.

Г. п. состоит в следующем. Пусть в кольце K(r, R) = {z : r < |z| < R}, 0 < r < R < ∞, имеется конечное число попарно непересекающихся односвязных областей В_k, k = 1, ... n, с жордановыми границами, содержащими невырождающиеся в точки дуги γ_k и Г_k соответствующих окружностей |z| = r, |z| = R [B_k образуют полосы, соединяющие граничные компоненты кольца K(r, R)]. Если B_k отображается на нек-рый прямоугольник {w : 0 < Re w < a_k, 0 < Im w < b_k} так, что γ_k и Г_k переходят в стороны длины a_k, то

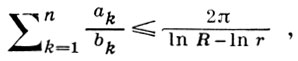
и равенство достигается только в том случае, если B_k = {z : r < |z| < R, α_k < arg z < β_k}, α_k, β_k - постоянные, k = 1, ..., n, и объединение B₁ ∪ ... ∪ B_n покрывает кольцо K(r, R), за исключением принадлежащих ему интервалов лучей arg z = α_k, arg z = β_k.

Г. и. и метод полос входят как составные части в экстремальной метрики метод и применяются не только в конформных, но и в более общих, напр., квазиконформных отображениях.

Лит : [1] Grötzsch Н., «Ber. Verhandl. Sächsisch. Akad. Wiss. Leipzig. Math.-naturwiss. Kl.», 1928, Bd 80, S. 367-76, 497-502; 1929, Bd 81, S. 217-21; 1930, Bd 82, S. 69-80; 1931, Bd 83, S. 185-200; 1932, Bd 84, S. 114-20; [2] Голузин Г. M., Геометрическая теория функций комплексного переменного, 2 изд., М., 1966; [3] Дженкинс Дж., Однолистные функции и конформные отображения, пер. с англ., М., 1962.

И. А. Александров.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.