ГРАФОВ ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ

ГРАФОВ ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ - функции, заданные на множестве графов и принимающие значения из нек-рого множества чисел. Ниже приведен ряд Г. ч. х. и их наиболее употребительные обозначения. Наиболее простыми Г. ч. х. являются число вершин и число ребер (дуг) графа G. Цикломатическим числом ν(G) графа G наз. наименьшее число ребер, удаление к-рых приводит к графу без циклов;

ν(G) = m - n + k,

где m - число ребер, n - число вершин, k - число компонент связности графа G. Числом вершинной связности א(G) [числом реберной связности λ(G)] наз. наименьшее количество вершин (ребер) графа G, удаление к-рых приводит к несвязному графу или тривиальному графу (т. е. графу, состоящему из одной вершины). Плотность φ(G) есть наибольшее число вершин в полном подграфе графа G; число независимости, или число внутренней устойчивости, ε(G) есть наибольшее число попарно несмежных вершин графа G (при этом попарно несмежные вершины графа G образуют внутренне устойчивое множество). Хроматическим числом χ(G) [реберным хроматическим числом χ'(G)] наз. наименьшее количество цветов, к-рыми можно раскрасить вершины (ребра) графа G так, чтобы любые смежные вершины (ребра) были окрашены разными цветами (см. также Графа раскраска). Числом внешней устойчивости β(G) наз. наименьшее количество вершин такого подмножества W множества вершин графа G, что любая вершина, не принадлежащая W, смежна по крайней мере с одной вершиной из W. Древесность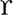

(G) есть наименьшее число непересекающихся по ребрам остовных лесов графа G, объединение к-рых есть граф G. Крупность ξ(G) - это наибольшее число непересекающихся по ребрам неплоскнх подграфов графа G. Толщина θ(G) - это наименьшее число плоских подграфов, объединение к-рых есть G. Число скрещиваний - это наименьшее число попарных пересечений ребер графа G при расположении его на плоскости. Род γ(G) графа G есть наименьший род двумерной ориентируемой поверхности, на к-рой можно уложить граф G без пересечения его ребер (см. Графа укладка).

Нек-рые числовые характеристики относят данному графу количества подграфов определенного типа, напр. число остовных деревьев, число гамильтоновых циклов и т. д. Существуют характеристики, зависящие от параметра f_k(G) (напр., число полных подграфов с к вершинами), совокупность этих характеристик может быть задана многочленом Σ_kf_k(G)x^k - аналогом производящей функции. Многие из таких многочленов можно находить рекуррентно, применяя операции над графами - удаление вершины или ребра, стягивание ребра и др. При решении задач теории графов часто возникает необходимость изучения взаимосвязи различных Г. ч. х. На нек-рых множествах Г. ч. х. достигают своих экстремальных значений, при нахождении к-рых часто удается описать графы, на к-рых они достигаются. Тогда нахождение экстремальных значений сводится к исследованию таких графов. Для изуяения графов, у к-рых рассматриваемая характеристика принимает заданное значение, оказывается полезным исследование свойств критических графов (см. Граф экстремальный).

Лит.: [1] Зыков А. А., Теория конечных графов, [в. 1], Новосиб., 1969: [2] Козырев В. П., в кн.: Итоги науки и техники. Сер. Теория вероятностей. Математическая статистика. Теоретическая кибернетика, т. 10, М., 1972, с. 25-75; [3] Xарари Ф., Теория графов, пер. с англ., М., 1973.

В. П. Козырев.

Источники:

Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.