ГРАФОВ ИЗОМОРФИЗМ

ГРАФОВ ИЗОМОРФИЗМ - отношение эквивалентности на множестве графов. Изоморфным отображением одного неориентированного графа на другой наз. взаимно однозначное отображение вершин и ребер одного графа соответственно на вершины и ребра другого графа, при к-ром сохраняется отношение инцидентности. Два графа наз. изоморфными, если существует изоморфное отображение одного из этих графов на другой. Графы G₁ и G₂, представленные на рис., не изоморфны, a G₁ и G₃ изоморфны. Обычно изоморфные графы не различают. Число попарно неизоморфных графов с данным числом вершин и данным числом ребер конечно. Подобным образом можно определить изоморфизм ориентированных графов, гиперграфов и сетей.

Проблема установления Г. и. является важной проблемой теории графов. Для нек-рых классов графов имеются алгоритмы, позволяющие установить изоморфизм достаточно эффективно (напр., для деревьев или плоских графов, см. [1]).

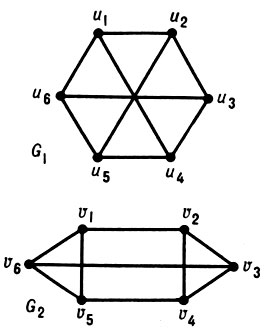
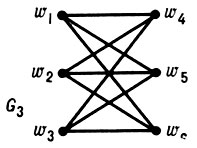
Для нек-рых классов графов с n вершинами доказана однозначная (с точностью до изоморфизма) восстанавливаемость графа по набору всех его (n - 1)-вершинных подграфов G - v, получаемых удалением всевозможных вершин v. Это установлено, в частности, для деревьев и турниров (при n ≠ 5,6).

Лит.: [1] Xопкрофт Дж., Тарьян Р., «Кибернетический сборник», 1975, в. 12, с. 39-61; [2] Kelly P. J., «Pacific J. Math.», 1957, v. 7, p. 961-68.

В. Б. Алексеев.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.