ГРАФА УКЛАДКА

ГРАФА УКЛАДКА, графа вложение, - отображение вершин и ребер графа соответственно в точки и непрерывные кривые нек-рого пространства такое, что вершины, инцидентные ребру, отображаются в концы кривой, соответствующей этому ребру. Правильной укладкой наз. укладка, при к-рой разным вершинам соответствуют различные точки, а кривые, соответствующие ребрам (исключая их концевые точки), не проходят через точки, соответствующие вершинам, и не пересекаются. Любой граф допускает правильную укладку в трехмерное пространство. Граф, допускающий правильную укладку на плоскости, наз. плоским. Существуют неплоские графы, напр. графы K₅ и K_3,3 (см. Граф плоский, рис. 1). Наименьший род двумерной ориентируемой поверхности, на к-рой граф G допускает правильную укладку, наз. родом γ(G) графа G. Установлено, в частности, что

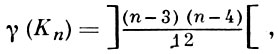
где K_n - полный граф с n вершинами, ]а[ - наименьшее целое число, не меньшее а;

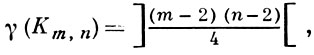
где K_m,n - полный граф двудольный;

γ(Q_n) = 1 + (n - 4) ⋅ 2^n-3,

где Q_n есть n-мерный куб. Толщиной θ(G) графа G наз. наименьшее число его плоских подграфов, объединение к-рых дает граф G. Установлено, в частности, что

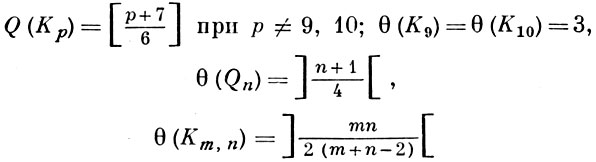
(возможно с несколькими исключениями).

Изучаются также другие числовые характеристики, связанные с Г. у., напр. число скрещиваний - наименьшее число пересечений ребер, с к-рым можно уложить данный граф на данной поверхности; крупность - наибольшее число непересекающихся по ребрам неплоских подграфов в данном графе и др. Рассматриваются также укладки на неориентируемых поверхностях. Вложение графа в n-мерную целочисленную решетку - это отображение в данную решетку, при к-ром вершины отображаются в различные узлы решетки, а ребра идут по линиям решетки.

Задачи об укладках графов на поверхностях и вложениях их в решетки возникают при автоматизированном проектировании ЭВМ, при проектировании коммуникаций и т. д.

Лит.: [1] Xарари Ф., Теория графов, пер. с англ., М., 1973; [2] Теория графов. Покрытия, укладки, турниры, сб. переводов, М., 1974, с. 82-159.

В. Б. Алексеев,

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.