ГРАФ ПЛОСКИЙ

ГРАФ ПЛОСКИЙ, планарный граф,- граф, допускающий правильную укладку на плоскости (см. Графа укладка). Иными словами, граф G наз. плоским, если он может быть изображен на плоскости так, что вершинам соответствуют различные точки плоскости, а линии, соответствующие ребрам (исключая их концевые точки), не проходят через точки, соответствующие вершинам, и не пересекаются. К рассмотрению Г. п. сводятся такие задачи, как задача о раскраске карт, задачи о проектировании коммуникаций, задачи из радиоэлектроники, связанные с реализацией схемы с помощью плоских печатных подсхем, и др. Любая правильная (без пересечения ребер) укладка связного Г. п. порождает разбиение плоскости на отдельные области (грани). Такое разбиение плоскости наз. плоской картой. Для любой плоской карты имеет место формула Эйлера

n - m + r = 2,

где n - число вершин, m - число ребер и r - число областей карты (включая внешнюю область). Отсюда графы K₅ (полный граф с n = 5) и K_3,3(полный граф двудольный, имеющий по 3 вершины в каждой доле, см. рис. 1) не являются плоскими. Эти графы являются в нек-ром смысле минимальными неплоскими графами в силу теоремы Понтрягина-Куратовского: граф плоский тогда и только тогда, когда он не содержит подграфа, гомеоморфного графу K₅ или K_3,3 (см. Графов гомеоморфизм).

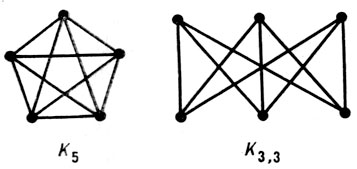
Рис. 1.

Существуют и другие критерии планарности (т. е. свойства графа быть плоским). В частности, граф G является плоским тогда и только тогда, когда каждая нетривиальная двусвязная компонента графа G обладает таким базисом циклов Z₁, ..., Z_m и таким дополнительным циклом Z₀, что любое ребро G принадлежит точно двум из этих m + 1 циклов (баз и с циклов - это подмножество циклов данного графа, независимое и полное во множестве всех циклов графа относительно операции сложения по модулю 2, см. Граф).

Любой Г. п. можно изобразить на плоскости так, чтобы все его ребра являлись отрезками прямых. Любой трехсвязный Г. п. (см. Графа связность) единственным образом укладывается на сфере (с точностью до гомеоморфизма сферы). Каждой укладке Г. п. на плоскости, а следовательно и плоской карте, можно поставить в соответствие геометрически двойственный ей граф, получаемый следующим образом. В каждую область карты помещается по вершине Г. п., и если две области имеют общее ребро е, то помещенные в них вершины соединяются ребром е^*, пересекающим только ребро е (на рис. 2 сплошными линиями изображена укладка Г. п., а штриховыми -двойственный ей граф). Плоская карта, каждая грань к-рой ограничена тремя ребрами, наз. плоской триангуляцией. Число ребер плоской триангуляции с n вершинами равно 3n - 6.

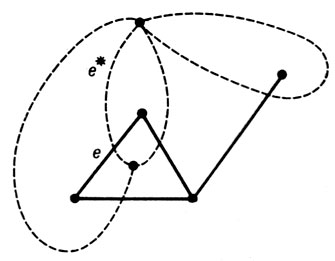
Рис. 2

В теории графов большое внимание уделяется раскраскам Г. п. (см. Графа раскраска); для неплоских графов изучаются различные числовые характеристики, показывающие степень непланарности, напр. род, толщина, крупность графа, число скрещиваний и др. (см. Графа укладка).

Лит.: [1] Xарари Ф., Теория графов, пер. с англ., М., 1973.

В. Б. Алексеев.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.