ГРАФ

ГРАФ - множество V вершин и набор Е неупорядоченных и упорядоченных пар вершин; обозначается Г. через G(V, Е). Неупорядоченная пара вершин наз. ребром, упорядоченная пара - дугой. Г., содержащий только ребра, наз. неориентированным; Г., содержащий только дуги, - ориентированным. Пара вершин может соединяться двумя или более ребрами (дугами одного направления), такие ребра (дуги) наз. кратными. Дуга (или ребро) может начинаться и кончаться в одной и той же вершине, такая дуга (ребро) наз. петлей. (Иногда под Г. понимают Г. без петель и кратных ребер; тогда Г., в к-ром допускаются кратные ребра, наз. мультиграфом, а Г., в к-ром допускаются кратные ребра и петли, наз. псевдографом.)

Вершины, соединенные ребром или дугой, наз. смежными. Ребра, имеющие общую вершину, также наз. смежными. Ребро (дуга) и любая из его двух вершин наз. инцидентными. Говорят, что ребро (u, v) соединяет вершины u и v, а дуга (u, v) начинается в вершине u и кончается в вершине v.

Каждый Г. можно представить в евклидовом пространстве множеством точек, соответствующих вершинам, к-рые соединены линиями, соответствующими ребрам (или дугам) Г. В трехмерном пространстве любой Г. можно представить таким образом, что линии, соответствующие ребрам (дугам), не пересекаются во внутренних точках.

Существуют различные способы задания Г. Пусть u₁, ..., u_n - вершины графа G(V, Е), а e₁, ..., e_m - его ребра. Матрицей смежности, соответствующей графу G, наз. матрица А = ||а_ij||, у к-рой элемент а_ij равен числу ребер (дуг), соединяющих вершины u_i и u_j (идущих из u_i в u_j), и а_ij = 0, если соответствующие вершины не смежны. В матрице инцидентности В = ||b_ij|| графа G элемент b_ij = 1, если вершина u_i инцидентна ребру е_j, и b_ij = 0, если вершина u_i и ребро е_j не инцидентны. Г. можно задать посредством списков, напр., указанием пар вершин, соединенных ребрами (дугами), или заданием для каждой вершины множества смежных с ней вершин. Два графа G(V, Е) и H(W, I) наз. изоморфными, если существует взаимно однозначное соответствие между множествами вершин V, W и множествами ребер Е, I, сохраняющее отношение инцидентности (см. также Графов изоморфизм).

Подграфом G'(V, Е') графа G(V, Е) наз. Г. с множеством вершин V' ⊆ V и множеством ребер (дуг) Е' ⊆ Е, каждое из к-рых инцидентно только вершинам из V. Подграфом G'(V', Е'), порожденным подмножеством V' ⊆ V, наз. Г. с множеством вершин V' и набором ребер (дуг) Е', состоящим из всех ребер (дуг) графа G, к-рые соединяют вершины из V'. Остовный подграф G'(V, Е') содержит все вершины графа G и нек-рый поднабор его ребер (дуг) Е ⊆ Е. Последовательность ребер (u₀, u₁), (u₁, u₂), ..., (u_i-1, u_i), (u_i u_i+1), ..., (u_r-1, u_r) наз. маршрутом, соединяющим вершины u₀ и u_r. Маршрут замкнут, если u₀ = u_r. Маршрут наз. цепью, если все его ребра различны, и простой цепью, если все его вершины различны. Замкнутая (простая) цепь наз. (простым) циклом. Г. наз. связным, если любая пара его вершин соединена маршрутом. Максимальный связный подграф графа G наз. компонентой связности. Несвязный Г. имеет по крайней мере две компоненты связности (см. также Графа связность).

Длина маршрута (цепи, простой цепи) равна количеству ребер в порядке их прохождения. Длина кратчайшей простой цепи, соединяющей вершины u_i и u_j в графе G, наз. расстоянием d(u_i, u_j) между u_i и u_j. В связном неориентированном Г. расстояние удовлетворяет аксиомам метрики. Диаметр Г. - это его наибольшее расстояние. Величина min_ui max_uj d(u_i, u_j) наз. радиусом, а вершина u₀, для к-рой max_uj d(u_i, u_j) принимает наименьшее значение, наз. центром графа G. В Г. может быть много центров и ни одного.

Степенью вершины u_i графа G, обозначаемой d_i, наз. число ребер, инцидентных этой вершине. Если граф G (без петель) имеет n вершин и m ребер, то d₁ + ... + d_n = 2m. Вершина u_i наз. изолированной, если d_i = 0, и концевой, если d_i = 1. Г., у к-рого все вершины имеют одинаковые степени (равные k), наз. регулярным (степени k). В полном Г. нет петель и каждая пара вершин соединена в точности одним ребром. Для графа G(V, Е), не имеющего петель и кратных ребер, дополнительным Г. к G наз. граф G̅(V̅, Е̅), у к-рого V̅ = V и вершины смежны в G̅ только в том случае, когда они не смежны в G. Г., дополнительный к полному, состоит из изолированных вершин и наз. пустым. Многие характеристики для графа G и его дополнения G̅ оказываются зависимыми. В ориентированном графе G для каждой вершины u_i определяются полустепень исхода и полустепень захода как количества дуг, выходящих из этой вершины и входящих в нее соответственно. Полный ориентированный Г. наз. турниром.

Каждому графу G можно отнести ряд Г., являющихся производными от G. Так, реберным графом L(G) графа G наз. Г., вершины к-рого соответствуют ребрам графа G и две вершины смежны в L(G) в том и только в том случае, когда соответствующие им ребра графа G смежны. В тотальном графе Т(G) графа G вершины соответствуют элементам графа G, т. е. вершинам и ребрам, и две вершины в Т(G) смежны тогда и только тогда, когда соответствующие элементы в G смежны или инцидентны. Многие свойства графа G переносятся на графы L(G) и T(G). Известно много обобщений понятия «Г.»; одними из них являются понятия гиперграфа и сети.

С помощью различных операций можно строить Г. из более простых, переходить от одного Г. к более простому, разбивать Г. на более простые, в заданном классе Г. переходить от одного Г. к другому и т. д. Наиболее употребительными одноместными операциями являются: удаление ребра (вершины ребра сохраняются), добавление ребра между двумя вершинами Г., удаление вершины вместе с инцидентными ей ребрами (Г., полученный в результате удаления вершины v из графа G, часто обозначают G - v), добавление вершины (к-рую можно соединить ребрами с нек-рыми вершинами Г.), стягивание ребра - отождествление пары смежных вершин, т. е. удаление пары смежных вершин и добавление новой вершины, смежной с теми вершинами Г., к-рые были смежны хотя бы с одной из удаленных вершин; подразбиение ребра - удаление ребра и добавление новой вершины, к-рая соединяется ребром с каждой вершиной удаленного ребра.

В ряде задач теории Г. используются двуместные операции над Г. Пусть G₁ = G(V₁, Е₁) и G₂ = G(V₂, Е₂) - Г. такие, что V₁ ∩ V₂ = ∅ и Е₁ ∩ Е₂ = ∅. Объединением графов G₁ и G₂ наз. граф G = G₁ ∪ G₂ с множеством вершин V = V₁ ∪ V₂ и множеством ребер E = E₁ ∪ Е₂. Произведением графов G₁ и G₂ наз. граф G = G₁ × G₂, множеством вершин к-рого являются элементы декартова произведения V = V₁ × V₂, причем две из этих вершин (u₁, u₂) и (v₁, v₂) смежны в том и только в том случае, если либо u₁ = u₂ и вершина u₂ смежна с вершиной v₂, либо u₂ = v₂ и вершина u₁ смежна с вершиной v₁. Напр., любой Г. является объединением своих компонент связности; Г., известный как n-мерный единичный куб Q_n, может быть определен рекуррентно с помощью операции произведения:

Q_n = K₂ × Q_n-2,

где Q₁ = K₂ - граф, состоящий из пары вершин, соединенных одним ребром. Эти операции можно определить также для пересекающихся Г., в частности для подграфов одного Г. Сложением по модулю 2 графов G₁ и G₂ наз. граф G с множеством вершин V = V₁ ∪ V₂ и множеством ребер Е = (Е₁ ∪ E₂)\(E₁ ∩ E₂).

Употребляются и другие многоместные операции над Г. Для некоторых классов Г. удается найти простые операции, позволяющие с помощью многократного их применения перейти от любого Г. изучаемого класса к любому другому Г. этого класса. На рис. 1 приведена операция, с помощью к-рой в классе Г. с одинаковым набором степеней можно перейти от одного произвольного Г. к любому другому; на рис. 2 показана операция, позволяющая в классе плоских триангуляции (см. Граф плоский) с одинаковым числом вершин перейти от произвольной триангуляции к любой другой Для описания и изучения нек-рых классов Г. отыскиваются такие операции и множества Г., из к-рых с помощью данных операций можно получить любой Г. заданного класса. Операции над Г. используются так же для построения Г. с заданными свойствами, при вычислении графов числовых характеристик и т. д.

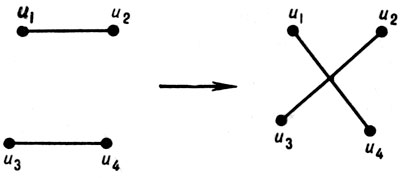
Рис. 1

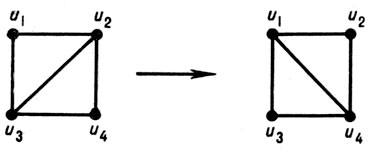
Рис. 2

Понятие «Г.» используется в определении таких математич. понятий, как управляющая система, в нек-рых определениях алгоритма, грамматики и др. Изложение ряда математич. теорий становится более наглядным при использовании геометрич. представления Г., напр. теории марковских цепей. Понятие «Г.» широко используется при создании и описании различных математич. моделей в экономике, биологии и т. д.

Лит.: [1] Берж К., Теория графов и ее применения, пер. с франц., М., 1962; [2] Оре О., Теория графов, пер. с англ., М., 1968; [3] Зыков А. А., Теория конечных графов, [в. 1], Новосиб., 1969; [4] Xарари Ф., Теория графов, пер. с англ., М., 1973.

В. П. Козырев.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.