ГРАССМАНА МНОГООБРАЗИЕ

ГРАССМАНА МНОГООБРАЗИЕ - множество G_n,m(k), m ≤ n, всех m-мерных подпространств в n-мерном векторном пространстве V над телом k. Если k - поле, то G_n,m(k) с помощью грассмановых координат (см. Внешняя алгебра) вкладывается в (C^m_n - 1)-мерное проективное пространство над к в виде компактного алгебраич. многообразия. В изучении геометрич. свойств Г. м. большую роль играют так наз. многообразия Шуберта S_a0a1...am, 0 ≤ a₀ < a₁ < ... < а_m ≤ n, определяемые следующим образом: если 0 = V₀ ⊂ V₁ ⊂ ... ⊂ V_n = V - флаг подпространств, т. е. набор таких подпространств, что dim V_k = k, то

S_a0a1...am = {W ∈ G_n,m(k), dim(W ∩ V_ar) ≥ r, 0 ≤ r ≤ m}.

Любое ρ-мерное алгебраич. подмногообразие в Г. м. G_n,m(k) эквивалентно единственной целочисленной линейной комбинации многообразий S_a0a1...am, где

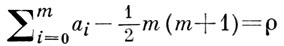
(см. [1]).

В случаях, когда k - поле действительных чисел ℝ, поле комплексных чисел ℂ или тело кватернионов ℍ, Г. м. над k можно рассматривать как компактное аналитич. многообразие (действительное при k = ℝ и ℍ и комплексное при k = ℂ). Эти многообразия замечательны тем, что являются классифицирующими пространствами для классических групп O(m), U(m), Sp(m) соответственно. Точнее, для любого клеточного комплекса X размерности ≤с(n + 1) - 2, где с = 1, 2, 4 соответственно, множество классов изоморфных m-мерных векторных расслоений над k с базой X находится в естественном взаимно однозначном соответствии с множеством гомотопич. классов непрерывных отображений X → G_n+m,m(k) (см. [2]). Аналогичная теория для групп SO(m) и SU(m) приводит к рассмотрению Г. м. G⁰_n,m(k) (k = ℝ или ℂ) ориентированных m-мерных подпространств в kⁿ. Перечисленные Г. м. тесно связаны, в частности, с теорией характеристических классов.

Роль, к-рую играют Г. м. в топологии, потребовала детального изучения их топологич. инвариантов. Старейший метод этого изучения основан на многообразиях Шуберта, с помощью к-рых легко построить клеточное разбиение для G_n,m(k) (k = ℝ, ℂ, ℍ). Оказывается, в частности, что циклы S_a0a1...am порождают базисы групп гомологии H_*(G_n,m(ℂ), ℤ), H_*(G_n,m(ℝ), ℤ₂), H_*(G_n,m(ℍ), ℤ). Хорошо изучены также алгебры когомологий Г. м. и действие степеней Стинрода на них [3].

Другой аспект теории Г. м. состоит в том, что они являются однородными пространствами линейной группы над соответствующим телом и представляют собой основные примеры неприводимых симметрических пространств.

Многообразия, аналогичные Г. м., можно конструировать также из подпространств бесконечномерных векторных пространств. В частности, в теории деформаций аналитич. структур существенную роль играет банахово аналитич. многообразие G_B, элементами к-рого являются замкнутые подпространства банахова пространства В над ℂ, допускающие замкнутое прямое дополнение.

Лит.: [1] Xодж В., Пидо Д., Методы алгебраической геометрии, пер. с англ., т. 2, М., 1954; [2] Xьюзмоллер Д., Расслоенные пространства, пер. с англ., М., 1970; [3] Расслоенные пространства и их приложения, М., 1958; [4] Чжэнь Шэн-шэнь, Комплексные многообразия, пер. с англ., М., 1961.

А. Л. Онищик.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.