ГРАМА-ШАРЛЬЕ РЯД

ГРАМА-ШАРЛЬЕ РЯД - ряд, определяемый выражением

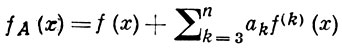
(1)

или

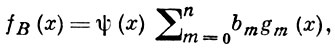
(2)

где х - нормированное значение случайной величины.

Ряд (1) наз. Г.-Ш. р. типа А; здесь

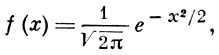
f^(k)(x) есть k-я производная от f(x), к-рую можно представить в виде

f^(k)(x) = (-1)^kH_k(х)f(х),

где H_k(x) - многочлены Чебышева-Эрмита. Производные f^(k)(x) и многочлены Н_k(х) обладают свойствами ортогональности, благодаря чему коэффициенты а_k можно определить при помощи основных моментов r_k данного ряда распределения. Ограничиваясь первыми членами ряда (1), получают

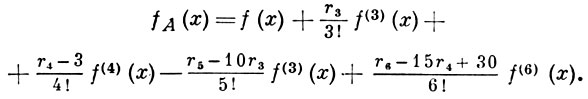
Ряд (2) наз. Г.- Ш. р. типа В; здесь

ψ(x) = λ^x/x! е^-λ, х = 0, 1, 2, ...,

а g_m(x) - многочлены, аналогичные многочленам Н_k(х

Ограничиваясь первыми членами ряда (2), получают

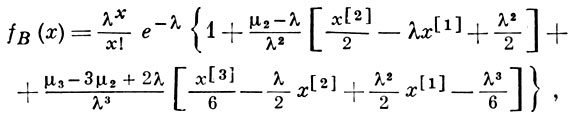
где μ_i - центральные моменты распределения, а х^[i] = х(х - 1) ... (x - i + 1).

Г.-Ш. р. были получены Дж. Грамом [1] и К. Шарлье [2] при исследовании функции вида

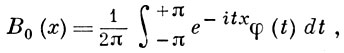
принятой для интерполирования между значениями

- общего члена биномиального распределения, где

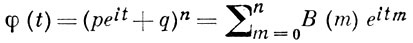
- характеристическая функция биномиального распределения. Разложение ln φ(t) по степеням t приводит к Г.- Ш. р. типа А для В₀(х), а разложение ln φ(t) по степеням р приводит к Г.-Ш. р. типа В.

Лит.: [1] Gram J. P., «J. reine und angew. Math.», 1883, Bd 94, S. 41-73; [2] Charlier С. V. L., «Arkiv Mat., Astr., Fys.», 1914, b. 2, № 25, s. 1-17; [3] Mитpoпольский А. К., Кривые распределения, Л., 1960.

А. К. Митрополъский.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.