ГРАМА ОПРЕДЕЛИТЕЛЬ

ГРАМА ОПРЕДЕЛИТЕЛЬ - определитель вида

Г = Г(a₁, ..., a_n) = det |(а_i, a_k)|, i, k = 1, ..., n,

где a₁, ..., a_n - элементы (пред)гильбертова пространства, а (a_i, a_k) - их скалярные произведения. Г. о. равен квадрату n-мерного объема параллелотопа, построенного на векторах a₁, ..., a_n.

Г. о. является определителем неотрицательной эрмитовой формы

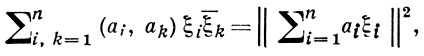
откуда и вытекают его основные свойства:

1) Г. о. неотрицателен, т. е. Г ≥ 0. Равенство Г = 0 имеет место тогда и только тогда, когда векторы линейно зависимы. Это свойство может рассматриваться как обобщение Коши неравенства:

Г(а₁, а₂) ≥ 0 пли (a₁, а₁) (а₂, а₂) ≥ (а₁, а₂) (а₂, а₁) = |(а₁, а₂)|².

В частности, Г. о. равен нулю, если какой-либо его главный минор (также являющийся Г. о.) равен нулю.

2) Г(a₁, ..., a_n) ≤ Г(a₁, ..., a_p) Г(a_p+1, ..., a_n),

причем равенство имеет место тогда и только тогда, когда подпространства L(a₁, ..., a_p) и L(a_p+1, ..., a_n) ортогональны или один из определителей Г(a₁, ..., a_p), Г(a_p+1, ..., a_n) равен нулю. Геометрически это неравенство означает, что объем параллелотопа не превосходит произведения объемов дополнительных граней. В частности,

Г(a₁, ..., a_n) ≤ Г(а₁) ... Г(а_n).

3) Г(a₁, ..., a_n) = Г(a₁, ..., a_n-1)h²,

где

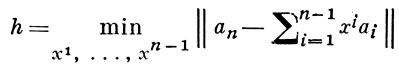
есть расстояние от элемента а_n до подпространства L(a₁, ..., a_n-1), т. е. наилучшее квадратическое приближение элемента a_n полиномами вида ∑^n-1_i=1xⁱa_i.

Если a₁, ..., a_n суть n-мерные векторы а_i =(а¹_i, ..., aⁿ_i), то

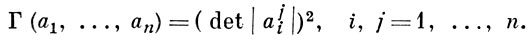
Г. о. введены И. П. Грамом [1] и независимо К. А. Андреевым (см. [2]) в связи с задачами разложения функций в ортогональные ряды и наилучшего квадратического приближения функций.

Г. о. применяются при решении многих задач линейной алгебры и теории функций: исследовании линейной зависимости системы векторов или функций, ортогонализации системы функций, построение проекторов, а также при изучении свойств систем функций. См. также Грама матрица.

Г. о. являются частным случаем определителей вида

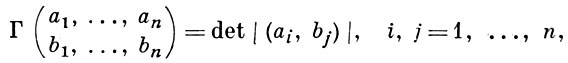
к-рые эрмитово билинейны по отношению к векторам а_i и b_j. Если а_i(х) принадлежат классу L₂(E), то справедлива формула

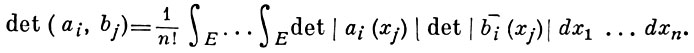
Лит.: [1] Gram J. P., On Rækkeudviklinger bestemte ved Hjælp of de mindste Kvadraters Methode, Kopenh., 1879; [2] Андреев К. А., Избр. работы, Харьков, 1955; [3] Гантмахер Ф. Р., Теория матриц, 3 изд., М., 1967.

Л. П. Купцов.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.