
ГРАДУИРОВАННАЯ АЛГЕБРА
ГРАДУИРОВАННАЯ АЛГЕБРА - алгебра А, аддитивная группа к-рой представлена в виде (слабой) прямой суммы групп Ai, i = 0, 1, 2, ..., причем AiAj ⊆ Ai+j для любых i, j. Таким образом аддитивная группа Г. а. (рассматриваемая как модуль над кольцом целых чисел) есть положительно градуированный модуль. Примером Г. а. может служить алгебра A = F[х] многочленов над полем F, где Ai - подпространство, порожденное одночленами степени i (A0 = F). Возможно более общее определение Г. а. А как такой алгебры, аддитивная группа к-рой представляется в виде прямой суммы групп Аα, где α пробегает нек-рую коммутативную полугруппу G и АαАβ ⊆ Aα+β для любых α, β ∈ G. С понятием Г. а. тесно связано понятие фильтрованной алгебры. Действительно, на каждой Г. a. A = ∑i≥0 естественным образом определяется возрастающая фильтрация:
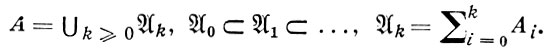
Обратно, если A = ∪k≥0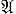 k - фильтрованная алгебра (
k - фильтрованная алгебра (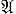 0 ⊂
0 ⊂ 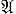 1 ⊂ ...,
1 ⊂ ..., 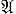 i
i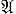 j ⊂
j ⊂ 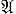 i+j), то определяют Г. а. GA = ∑i≥0Ai (Ai =
i+j), то определяют Г. а. GA = ∑i≥0Ai (Ai = 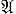 i/
i/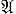 i-1, A0 =
i-1, A0 = 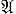 0), к-рую наз. Г. а., ассоциированной с А. Аналогично определяется градуированное кольцо.
0), к-рую наз. Г. а., ассоциированной с А. Аналогично определяется градуированное кольцо.
Е. Н. Кузьмин.
Источники:
- Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'