ГРАДИЕНТНОЕ ПРЕОБРАЗОВАНИЕ

ГРАДИЕНТНОЕ ПРЕОБРАЗОВАНИЕ - преобразование в классической и квантовой теории поля, к-рое изменяет характеристики поля, не являющиеся наблюдаемыми (напр., потенциалы поля), и не меняет при этом имеющие физич. смысл наблюдаемые величины (напр., напряженности поля). Название «Г. п.» возникло в классич. теории электромагнитного поля, где 4-мерный вектор электромагнитного потенциала А_n(х), n = 0, 1, 2, 3, вводится в теорию неоднозначным образом, поскольку так наз. Г. п. 2-го рода:

А_n(x) → А'_n(х) = А_n(х) + ∂f(x)/∂xⁿ (1)

с произвольной функцией f(x), обладающей частными производными 1-го и 2-го порядков, не сказываются на значениях компонент антисимметричного тензора электромагнитного поля

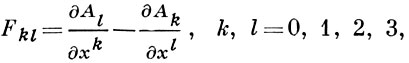
к-рые равны физически наблюдаемым компонентам векторов напряженности электрич. поля E_α = F_α0, α = 1, 2, 3, и магнитного поля H₁ = F₂₃; H₂ = F₃₁; H₃ = F₁₂. При Г. п. 2-го рода остаются неизменными уравнения поля

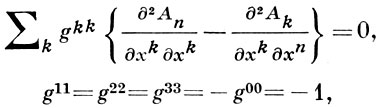
т. е. имеет место свойство так наз. градиентной инвариантности теории поля. С помощью соответствующего выбора функции f(x) можно добиться выполнения для А к.-л. дополнительного условия, к-рое наз. условием калибровки, что позволяет упростить вид уравнений поля. Напр., линейное относительно потенциала А условие Лоренца - равенство нулю 4-мерной дивергенции

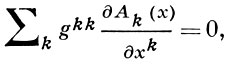
приводит к уравнению Д'Аламбера для А_n(х) (см. Д'Аламбера оператор)

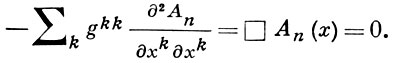
Условие Лоренца не определяет полностью потенциал А, так как в теории остается инвариантность относительно так наз. специализированного Г. п. 2-го рода (1) с функцией f₀(x), удовлетворяющей уравнению Д'Аламбера: □f₀(x) = 0. Однако при определенном выборе f₀(x) (так наз. лоренцева система отсчета) можно добиться выполнения условия A₀ = 0. При этом условие Лоренца (2) сводится к условию div A = 0 для 3-мерного вектор-потенциала, т. е. к условию поперечности электромагнитного поля. В случае комплексных полей должна иметь место также инвариантность теории относительно Г. п. 1-го рода для волновых функций поля и их производных

Ф(х) → Ф'(х) = e^iαФ(х); Ф*(х) → Ф*'(х) = е^-iαФ*(х), (4)

так как все наблюдаемые динамич. величины в силу условия действительности (эрмитовости) должны выражаться только через действительные билинейные относительно Ф* и Ф формы. Условие инвариантности теории поля относительно Г. п. 1-го рода в силу общих принципов механики означает существование нек-рых сохраняющихся наблюдаемых физич. величин - зарядов, к-рые выражаются через функции поля, или, иначе говоря, существование законов сохранения этих зарядов. Соответствующие лагранжианы и уравнения поля должны быть инвариантны относительно Г. п., иначе называемых калибровочными преобразованиями. Напр., в случае взаимодействующих с электромагнитным полем А_n(х) комплексных полей ψ(х), соответствующих частицам, обладающим электрич. зарядом, лагранжианы свободных полей и лагранжиан взаимодействия и уравнения поля должны быть инвариантны относительно калибровочных преобразований вида

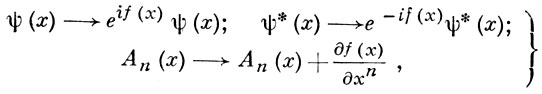
(5)

т. е. относительно Г. п. (1) и (4), где фазовый множитель в (4) может зависеть от 4-мерных координат пространства-времени и должен совпадать с произвольной скалярной функцией, входящей в (1). В этом случае в системе полей А_n(х) и ψ(х) выполняется закон сохранения электрич. заряда. Калибровочные преобразования (5) образуют абелеву группу преобразований в том смысле, что калибровочная функция f(x) = g(x) + h(x) описывает калибровочное преобразование, представляющее собой два калибровочных преобразования с функциями g(x) и h(x), произведенных в любой последовательности. При построении более общих, чем рассмотренный пример, теорий взаимодействующих полей для выполнения соответствующих законов сохранения тех или иных зарядов необходимо требовать инвариантности лагранжианов и уравнений поля относительно неабелевых калибровочных преобразований, в к-рых калибровочные функции f(x) должны быть операторами.

Лит.: [1] Боголюбов Н. Н., Ширков Д. В., Введение в теорию квантованных полей, М., 1957.

В. Д. Кукин.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.