ГРАДИЕНТ

ГРАДИЕНТ - одно из основных понятий векторного анализа и теории нелинейных отображений.

Градиентом скалярной функции f(t) векторного аргумента t = (t¹, ..., tⁿ) из евклидова пространства Еⁿ наз. производная функции f(t) по векторному аргументу t, то есть n-мерный вектор с компонентами ∂f/∂tⁱ, 1 ≤ i ≤ n. Существуют следующие обозначения Г. функции f(t) в точке t₀:

grad f(t₀), ∇f(t₀). ∂f(t₀)/∂t f'(t₀).

Г. представляет собой ковариантный вектор: компоненты Г., вычисленные в двух различных координатных системах t = (t¹, ..., tⁿ) и τ = (τ¹, ..., τⁿ), связаны соотношениями:

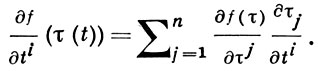
Вектор f'(t₀), начало к-рого помещено в точку t₀, указывает направление наискорейшего роста функции f(t), ортогональное линии или поверхности уровня функции f(t), проходящей через точку t₀.

Производная функции в точке t₀ в направлении произвольного единичного вектора N = (N¹, ..., Nⁿ) равна проекции Г. функции на это направление:

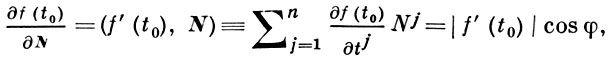
где φ - угол между N и f'(t₀). Максимум производной достигается при φ = 0, т. е. в направлении Г., и равен длине Г.

Понятие Г. тесно связано с понятием дифференциала функции. В случае дифференцируемости f(f) в точке t₀ вблизи t₀

f(t) = f(t₀) + (f'(t₀)), t - t₀) + o(|t - t₀|). (2)

то есть df = (f'(t₀), dt). Существование в точке t₀ Г. функции f(t) не достаточно для справедливости формулы (2).

Точка t₀, в к-рой f'(t₀) = 0, наз. стационарной (критической или экстремальной) точкой функции f(t). Такой точкой является, напр., точка локального экстремума функции f(t) и система ∂f(t₀)/∂t' = 0, 1 ≤ i ≤ n, используется для нахождения экстремальной точки t₀.

При вычислении значения Г. справедливы формулы:

grad(λf) = λ grad f, λ = const, grad (f + g) = grad f + grad g, grad (fg) = g grad f + f grad g, grad (f/g) = 1/g²(g grad f - f grad g).

Г. f'(t₀) есть производная в точке t₀ по объему векторной функции объема

Ф(E) = ∫_t∈∂E f(t)Mds,

тде Е - область с границей ∂Е, t₀ ∈ E, ds - элемент площади ∂Е, а M - единичный вектор внешней нормали к ∂Е. Другими словами

f'(t₀) = lim Ф(E)/объем E при E → t₀.

Формулы (1), (2) и перечисленные выше свойства Г. указывают на инвариантный относительно выбора системы координат характер понятия Г.

В криволинейной системе координат х = (x¹, ..., xⁿ), в к-рой квадрат длины элемента

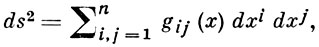
компоненты Г. функции f(x), отнесенного к ортам, касающимся координатных линий в точке х, равны

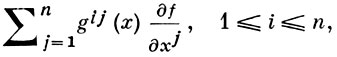
где матрица ||g^ij|| - обратная к матрице ||g_ij||.

Понятие Г. для более общих векторных функций векторного аргумента вводится при помощи равенства (2), означающего, что Г. есть линейный оператор, действием к-рого на приращение t - t₀ аргумента получается главная линейная часть приращения f(t) - f(t₀) вектор-функции f(f). Напр., если f(t) = (f¹(t), ..., f^m(t)) есть m-мерная вектор-функция аргумента t = (t¹, ..., tⁿ), то ее Г. в точке t₀ - Якоби матрица J = J(t₀) с компонентами ∂fⁱ/∂t^j(t₀), 1 ≤ j ≤ m, 1 ≤ j ≤ n, причем

f(t) = f(t₀) + J(t - t₀) + o(t - t₀),

где o(t - t₀) - m-мерный вектор, длина к-рого есть o(|t - t₀|). Матрица J определяется при помощи предельного перехода

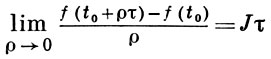
(3)

с любым фиксированным n-мерным вектором τ.

В бесконечномерном гильбертовом пространстве определение (3) равносильно определению дифференцируемости по Фреше и Г. при этом совпадает с производной Фреше.

В случае, когда f(t) лежит в бесконечномерном векторном пространстве, возможны различные типы предельного перехода в (3) (см., напр., Гато производная).

В теории тензорных полей, заданных в области n-мерного аффинного пространства связности, при помощи Г. описывается главная линейная часть приращения компонент тензора при соответствующем связности параллельном перенесении. Г. тензорного поля

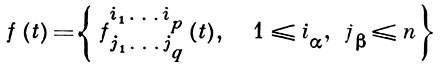
типа (р, q) есть тензор типа (р, q+1) с компонентами

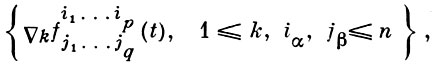
где ∇_k - оператор абсолютного (ковариантного) дифференцирования.

Понятие Г. широко применяется в различных задачах математики, механики и физики. Многие физич. поля могут быть рассматриваемы как градиентные поля (см. Потенциальное поле).

Лит.: [1] Кочин Н. Е., Векторное исчисление и начала тензорного исчисления, 9 изд., М., 1965; [2] Рашевский П. К., Риманова геометрия и тензорный анализ, 3 изд., М., 1967.

Л. П. Купцов.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.