ГОМОТОПИЧЕСКАЯ ГРУППА

ГОМОТОПИЧЕСКАЯ ГРУППА - обобщение фундаментальной группы, предложенное В. Гуревичем [1] в связи с задачей о классификации непрерывных отображений. Г. г. определены для любого n ≥ 1. При n = 1 Г. г. совпадает с фундаментальной группой. Определение Г. г. не конструктивно, и поэтому их вычисление является трудной задачей, общие методы решения к-рой были выработаны только в 50-х гг. 20 в. Значение Г. г. определяется тем, что все задачи теории гомотопий более или менее сводятся (см. Гомотопический тип) к задаче вычисления тех или иных Г. г.

Пусть

Iⁿ = {(t₁, ..., t_n); 0 ≤ t₁ ≤ 1, 0 ≤ t_n ≤ 1}

- единичный n-мерный куб, I^n-1 - его грань t_n = 0 и J^n-1 - объединение всех остальных его граней. Для любой пунктированной пары (X, А, х₀) (см. Пунктированный объект) символом π_n(X, А, х₀) (или просто π_n(Х, А)) обозначается пунктированное множество всех гомотопич. классов [u] (см. Гомотопия) отображений

u : (Iⁿ, I^n-1, J^n-1) → (X, A, x₀);

отмеченным элементом (нулем) этого множества служит класс постоянного отображения, переводящего весь куб I_n в точку х₀. Каждое непрерывное отображение

f : (X, A, x₀) → (Y, В, y₀)

индуцирует нек-рый морфизм

f_* : π_n(X, А, х₀) → π_n(Y, В, у₀)

пунктированных множеств. Для любого n ≥ 1 множества π_n(Х, А, х₀) и морфизмы f^* составляют нек-рый функтор π_n из категории пунктированных пар в категорию пунктированных множеств. Этот функтор гомотопически инвариантен, то есть f_* = g_*, когда f и g гомотопны (как отображения пунктированных пар). Кроме того, он нормирован, в том смысле, что если Х = А = х₀, то π_n(Х, А, х₀) = 0.

При n ≥ 2 в множество π_n(X, А, х₀) можно ввести операцию сложения, относительно к-рой оно будет группой (при n > 2 даже абелевой): по определению, если х = [u] и y = [v], то x + y = [w], где w - отображение

(Iⁿ, I^n-1, J^n-1) → (Х, А, х₀),

определенное формулой

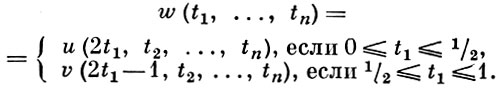
(1)

Получающаяся группа π_n(Х, A, х₀) наз. n-й гомотопической группой (или n-мерной Г. г.) пунктированной пары (X, А, х₀); говорят также о Г. г. пары (X, А) в точке х₀ или о Г. г. пространства X относительно подпространства А в точке х₀. Отображения являются гомоморфизмами этих групп. Таким образом, при n ≥ 2 можно считать, что функтор π_n принимает значения в категории групп (при n > 2 даже абелевых).

При А = х₀ группа π_n(Х, А, х₀) обозначается π_n(Х, х₀), или просто π_n(Х), и наз. абсолютной гомотопической группой пунктированного пространства (X, х₀) (или пространства X в точке х₀). Ее элементами являются гомотопич. классы отображений (Iⁿ, İⁿ) → (Х, х₀), где I˳ⁿ = I^n-1 ∪ J^n-1 - граница куба. Для таких отображений формула (1) имеет смысл и при n = 1, так что множество π₁(Х, х₀) оказывается группой. Эта группа совпадает с классической фундаментальной группой. Обычно групповая операция в π₁(Х, х₀) наз. умножением. Эта группа, вообще говоря, неабелева, тогда как группа π₂(Х, х₀) - абелева. Для любого n ≥ 1 группы π_n(Х, х₀) и соответствующие гомоморфизмы составляют нек-рый функтор из категории пунктированных пространств в категорию групп (при n > 1 - в категорию абелевых групп). Этот функтор является композицией π_n ○ ι функтора вложения ι : (X, x₀) → (Х, х₀, х₀) и построенного выше функтора π_n.

Функтор π_n ○ ι распространяется и на случай n = 0, если понимать под π₀(Х, х₀) пунктированное множество компонент линейной связности пространства X; нулем этого множества является компонента, содержащая точку х₀. Множество π₀(Х, А, х₀) при А ≠ х₀ не определяется. Для упрощения формулировок множества π₀(Х, х₀) и π₁(Х, А, х₀) обычно также наз. Г. г., хотя они, вообще говоря, являются лишь пунктированными множествами.

Для любого элемента х = [u] ∈ π_n(Х, А, х₀) отображение u | I^n-1 представляет собой отображение (I^n-1, I^n-1) → (A, х₀) и потому определяет нек-рый элемент Г. г. π_n-1(A, х₀). Этот элемент зависит только от х и обозначается символом ∂x. Получающееся отображение ∂ : π_n(Х, А, х₀) → π_n-1(А, х₀) является морфизмом пунктированных множеств (при n > 1 - гомоморфизмом групп) и наз. граничным гомоморфизмом, или граничным оператором. Граничный гомоморфизм вместе с гомоморфизмами и индуцированными вложениями i : (А, х₀) → (Х, х₀) и j : (X, х₀) → (Х, А, х₀), позволяет написать бесконечную слева последовательность групп и гомоморфизмов:

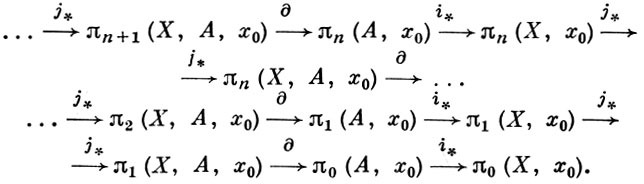
Это - точная последовательность; она наз. точной гомотопической последовательностью пары (X, А, х₀) и обозначается обычно π(X, А, х₀). Если π_n(Х, х₀) = 0 для всех n ≥ 0, то гомоморфизм ∂ : π_n(Х, А, х₀) →_n-1(А, х₀) является изоморфизмом (также для всех n).

Граничный гомоморфизм ∂ обладает свойством естественности, т. е. является морфизмом функтора π_n в функтор π_n ○ ι [точнее, в функтор π_n ○ ι', где ι' : (X, A, х₀) ↦ (A, х₀, х₀)]. Это позволяет определить π_n(Х, А, х₀) как функтор, принимающий значения в категории точных последовательностей пунктированных множеств, являющихся, за исключением последних шести множеств, абелевыми группами, а за исключением последних трех множеств, - группами.

Пусть р : Е → В - произвольное расслоение в смысле Серра и пусть А ⊂ В, Е' = р^-1(А), е₀ ∈ Е' и b₀ = р(е₀). Отображение р определяет нек-рое отображение р' : (E, Е', е₀) → (В, А, b₀) пунктированных пар. Для любого n ≥ 1 индуцированный этим отображением гомоморфизм р'_*: π_n(Е, Е', е₀) → π_n(В, А, b₀) является изоморфизмом. В частности, это верно при A = b₀. В этом случае формула τ = ∂ ○(р'_*)^-1 однозначно определяет нек-рый гомоморфизм τ : π_n(В, b₀) → π_n-1(F, е₀), где F = р^-1(b₀) - слой расслоения р над точкой b₀. Этот гомоморфизм наз. гомотопической трансгрессией. Он входит в точную последовательность

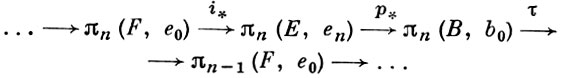
Эта последовательность наз. гомотопической последовательностью расслоения р : Е ↦ В. Сопоставление расслоению его гомотопич. последовательности приводит к нек-рому функтору на категории всех (пунктированных) расслоений.

В частном случае, когда р есть стандартное Серра расслоение путей над пространством X, для любого n ≥ 0 имеет место изоморфизм π_n(Ω, Х) ≈ π_n+1(Х), где ΩX -петель пространство пространства X. Этот изоморфизм наз. изоморфизмом Гуревича.

Перечисленные свойства по существу однозначно определяют Г. г. π_n(Х, А, х₀), т. е. могут быть приняты за аксиомы, описывающие эти Г. г. Именно, пусть π₁, ..., π_n, ... произвольная последовательность гомотопически инвариантных нормированных функторов, заданных на категории пунктированных пространств, принимающих значения в категории пунктированных множеств и обладающих тем свойством, что для любого расслоения в смысле Серра р : Е → В любого подмножества А ⊂ В и любой точки е₀ ∈ р^-1(А) индуцированный гомоморфизм π_n(Е, р^-1(А), е₀) → π_n(B, А, р(e₀)) является изоморфизмом. Такая последовательность наз. гомотопической системой, если для любого n ≥ 1 задан морфизм ∂ функтора π_n в функтор π_n ○ ι' (при n = 1 - в π₀(Х, х₀)), являющийся изоморфизмом для любой пунктированной пары (X, А, х₀), для которой π_n(Х, х₀) = 0 при всех n ≥ 0. Любая гомотопич. система изоморфна построенной выше гомотопич. системе, состоящей из Г. г. Более того, при n ≥ 3 в пунктированные множества π_n(Х, А, х₀) (а также в множества π₂(Х, x₀)) можно единственным образом ввести групповое строение (структуру группы) так, чтобы все морфизмы f_* были гомоморфизмами [это строение совпадает, стало быть, с тем, к-рое определяется формулой (1)]. В группах же π₂(Х, А, х₀) при А ≠ х₀ и π₁(Х, х₀) можно только ввести еще инверсную групповую операцию. Все это и означает, что перечисленные выше свойства однозначно определяют Г. г. (с точностью до порядка сомножителей в некоммутативных группах).

Для любого отображения u : (Iⁿ, İⁿ) → (Х, х₂) и любого пути v : I → Х, соединяющего точку х₁ с точкой х₂, формула g_t(x) = v(1 - t), х ∈ İⁿ, определяет нек-рую гомотопию отображения u|İⁿ. По аксиоме о распространении гомотопий (см. Корасслоение) эта гомотопия может быть распространена до нек-рой гомотопий u_t : Iⁿ → Х, обладающей тем свойством, что u₀ = u. Конечное отображение u₁ этой гомотопий переводит İⁿ в x₁, то есть представляет собой отображение (Iⁿ, İⁿ) → (Х, х₀). Соответствующий элемент Г. г. π_n(Х, х₁) зависит только от класса [u] ∈ π_n(Х, х₂) отображения u и гомотопич. класса α = [v] пути v и обозначается символом αх (при n = 1 - символом х^α). Семейство G_x = π_n(Х, х) определяется тем самым как локальное семейство на пространстве X, т. е. на фундаментальном группоиде этого пространства. В частности, для любой точки х₀ ∈ Х группа π₁(Х, х₀) оказывается группой операторов группы π_n(Х, х_n). При n = 1 эти операторы действуют как внутренние автоморфизмы: х^α = αхα^-1, а при n > 1 определяют группу π_n(Х, х₀) как π₁(Х, x₀)-модуль. Для любого непрерывного отображения f : (X, х₀) → (Y, y₀) индуцированные гомоморфизмы f_* : π_n(Х, х₀) → π_n(Y, у₀) являются операторными гомоморфизмами (гомоморфизмами модулей): f_*(αx) = f_*(α) f_*(х).

Аналогичным образом группы G_x = π_n(Х, А, х), х ∈ А составляют локальное семейство Г. г. на подпространстве А. В частности, π₁(A, х₀) является группой операторов Г. г. π_n(X, А, х₀), так что при n > 2 группа π_n(Х, А, х₀) будет π₁(А, х₀)-модулем. Группа π₂(Х, А, х₀) является скрещенным (π₁(A, х₀), ∂)-модулем (см. Скрещенные модули), где ∂ : π₂(Х, А, х₀) → π₁(А, х₀) - граничный гомоморфизм.

Группа π₁(А, х₀) служит группой операторов не только групп π_n(Х, А, х₀), но и групп π_n(А, х₀), а также, в силу естественного гомоморфизма π₁(А, х₀) → π₁(Х, х₀), -группой операторов групп π_n(Х, х₀). Относительно этого действия группы π₁(А, х₀) все гомоморфизмы точной последовательности π(Х, А, х₀) являются операторными гомоморфизмами, так что группа π₁(А, х₀) может рассматриваться как группа операторов последовательности π(Х, А, х₀). Это равносильно тому, что последовательности π(Х, А, х), х ∈ А составляют локальное семейство точных последовательностей на подпространстве А.

В случае, когда дополнение Х\А представляет собой объединение непересекающихся открытых n-мерных клеток, π₁(А, x₀)-модуль π_n(Х, А, х₀) является свободным модулем (при n = 2 - свободным скрещенным модулем) и обладает системой свободных образующих -базисом, находящимся в биективном (не обязательно естественном) соответствии с клетками из Х\А (теорема Уайтхеда).

Отображения (Iⁿ, İⁿ) → (Х, х₀) находятся в биективном соответствии с отображениями (Sⁿ, s₀)→ (X, х₀), где Sⁿ - произвольная д-мерная сфера, а s₀ - нек-рая ее точка; поэтому элементы группы π_n(Х, х₀) можно рассматривать как гомотопич. классы отображений (Sⁿ, s₀) → (X, х₀). Это верно и при n = 0. Указанное отождествление зависит от выбора нек-рого относительного гомеоморфизма φ : (Iⁿ, İⁿ) → (Sⁿ, s₀). Обычно сфера Sⁿ и гомеоморфизм φ предполагаются раз навсегда выбранными и фиксированными. В первоначальном, ставшем малоупотребительным определении Гуревича, сфера Sⁿ не фиксировалась, а гомеоморфизм φ задавался с точностью до гомотопий. Такое задание гомеоморфизма φ равносильно заданию нек-рой ориентации сферы Sⁿ. Таким образом, по Гуревичу, элементами группы π_n(Х, х₀) являются пунктированные гомотопич. классы отображений ориентированной n-мерной сферы в пространстве X. Множество [Sⁿ, X] непунктированных гомотопич. классов отображений Sⁿ → X находится в биективном соответствии с орбитами действия группы π₁(Х, х₀) в группе π_n(Х, х₀). Если π₁(Х, х₀) = 0 (или, более общим образом, если группа π₁(Х, х₀) тривиально действует на группе π_n(Х, х₀), - в этом случае пространство X наз. гомотопически n-простым), то π_n(Х, х₀) не зависит от точки х₀ (так что в этом случае обозначение π_n(Х) полностью оправдано). Эта группа естественным образом отождествляется с множеством [Sⁿ, X], к-рое является, стало быть, в этом случае группой. Пространство, гомотопически n-простое для всех n, наз. абелевым.

Пусть s_n - ориентирующий класс гомологии сферы Sⁿ и пусть h([f]) = f_*(s_n), [f] ∈ π_n(Х, х₀). Тем самым определяется нек-рый гомоморфизм h : π_n(Х, x₀) → H_n(Х), наз. гомоморфизмом Гуревича. Его ядро содержит все элементы вида αх - х, х ∈ π_n(Х, х₀), α ∈ π₁(Х, х₀) (при n = 1 - все элементы вида х^αх^-1 = αхα^-1х^-1, т. е. содержит коммутант [π₁, π₁] группы π₁(X, x₀)). Классич. теорема Пуанкаре утверждает, что при n = 1 ядро гомоморфизма h совпадает с коммутантом [π₁, π₁], так что группа Н₁(X) изоморфна прокоммутированной фундаментальной группе π₁(X, х₀). Обобщением теоремы Пуанкаре на случай n > 1 является теорема Гуревича, утверждающая, что если π_i(А) = 0 при i < n, то гомоморфизм h : π_n(Х) → Н_n(X) является изоморфизмом (а гомоморфизм h : π_n+1(Х) → H_n+1(Х) - эпиморфизмом).

Аналогичным образом элементы группы π_n(X, А, х₀) можно рассматривать как (пунктированные) гомотопич. классы отображений (Е, S) → (X, А), где Е -(ориентированный) n-мерный шар, а S - его граница. Если пара (X, A) гомотопически n-проста [т. е. группа π₁(A, х₀) тривиально действует на группе π_n(X, A, х₀)], то в этом определении пунктированность можно игнорировать. Формула

h([f]) = f_*(е_n),

где е_n - ориентирующий класс гомологии пары (Е, S), а [f] ∈ π_n(Х, А, х₀), определяет гомоморфизм Гуревича

h : π_n(Х, А, х₀) → Н_n(Х, А).

Если π₁(A, x₀) = 0 и π_n(Х, A, x₀) = 0 при i < n, то этот гомоморфизм является изоморфизмом (теорема Гуревича для относительных групп).

Для вычисления Г. г. конкретных пространств известны два основных метода: метод убивающих пространств и метод гомотопич. резольвент (см. Гомотопический тип, Постникова системы). Первый метод основывается на изоморфизме π_n+1(Х) ≈ H_n+1(X, n), вытекающем из теоремы Гуревича, и определении убивающего пространства (X, n). Этот изоморфизм сводит задачу вычисления группы π_n+1(X) к задаче вычисления групп гомологии H_n+1(Х, n). Пространство (X, n) расслаивается над пространством (X, n - 1) со слоем К(π_n(Х), n - 1), а группы гомологии пространств К(π, n) известны. Поэтому индукцией можно пытаться найти нужные группы гомологии убивающих пространств. Задача вычисления группы гомологии расслоенного пространства по группам гомологии его базы и слоя в общем виде полностью не решена (и, по-видимому, общего удовлетворительного решения не имеет), однако обширную информацию о группах гомологии пространств (X, n) можно извлечь из соответствующих спектральных последовательностей Серра. Во многих случаях этой информации достаточно для вычисления групп Н_n+1(Х, n) ≈ π_n+1(Х), по крайней мере для нек-рых n. Существенное технич. упрощение задачи достигается на основе серровской теории классов абелевых групп и вытекающей из этой теории теоремы G_p-аппроксимации, позволяющей проводить все вычисления во-первых для когомологий, а во-вторых лишь для групп коэффициентов ℤ/p. Геометрич. принципы, лежащие в основе этой техники, были недавно вскрыты Дж. Адамсом (J. Adams) и Д. Салливаном (D. Sullivan) [8] на основе понятия локализации топологич. пространств по данному простому р.

Второй (также индуктивный) метод вычисления Г. г. состоит в постепенном построении гомотопич. резольвенты пространства X. Пусть уже известен n-й член этой резольвенты [напр., если X = Sⁿ, то Х_n = K(ℤ, n)]. Следующий член Х_n+1 должен быть расслоенным пространством над Х_n со слоем K(π_n+1(Х), n+1), причем группа Н_n+1(Х_n+1) должна быть изоморфна известной группе Н_n+1(Х). Это дает (на основе соответствующей спектральной последовательности) определенную информацию о группе π_n+1(Х), позволяющую во многих случаях полностью ее вычислить. Напр., при X = Sⁿ этим методом можно найти группы π_n+1(Sⁿ) для всех k ≤ 13. В современной своей форме эти вычисления также основываются на понятии локализации.

Метод гомотопич. резольвент был доведен (см. [5]) до алгоритма, применимого к любому односвязному конечному клеточному разбиению и дающего все его Г. г. Однако этот алгоритм для практич. применения слишком сложен.

Поскольку гомотопич. теория пространств полностью эквивалентна гомотопич. теории симплициальных множеств, определение Г. г. может быть перенесено на любые (полные) симплициальные множества. Получающееся «комбинаторное» определение Г. г. (принадлежащее Д. Кану) легко может быть доведено до алгоритма. Однако и этот алгоритм для практич. вычислений слишком сложен.

Любой из описанных методов без труда устанавливает, что Г. г. произвольного односвязного пространства, имеющего конечно порожденные группы гомологий, также конечно порождены. Аналогичное утверждение для неодносвязных пространств (Г. г. конечно порождены как π₁(X)-модули), вообще говоря, неверно.

Пусть S - функтор (приведенной) надстройки, а Ω - функтор петель. Так как эти функторы сопряжены, то для любого X тождественное отображение SX → SX определяет нек-рое вложение X ⊂ ΩSX. Поскольку π_n(ΩSX) ≈ π_n+1(SX), это вложение определяет нек-рый гомоморфизм

Е : π_n(X) → π_n+1(SX),

известный как гомоморфизм надстройки. Он совпадает с гомоморфизмом, получающимся при сопоставлении произвольному (пунктированному) отображению f : Sⁿ → Х его надстройки Sf : Sⁿ⁺¹ → SX. Этот гомоморфизм входит в точную последовательность

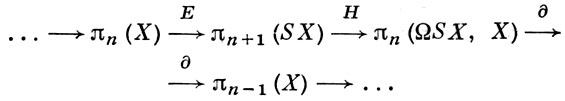
Эта последовательность наз. надстроечной последовательностью пространствах. Фигурирующий в ней гомоморфизм Н является обобщением классического Хопфа инварианта.

В случае, когда X - счетное одновершинное клеточное разбиение, пространство ΩSX может быть заменено (см. [7]) приведенной степенью Х_∞, разбиения X. Это показывает, что если π_i(Х) = 0 при i < m, то гомоморфизм Е является изоморфизмом для всех n < 2m - 1 и эпиморфизмом при n = 2m - 1. Эта теорема известна как теорема Фрейденталя о надстройке [Г. Фрейденталь (Н. Freudenthal) первым опубликовал доказательство для случая X = Sⁿ, хотя теорема была известна и ранее].

Теорема Фрейденталя показывает, что при k < 2n - 1 группа π_n+k(Sⁿ) не зависит от n. Она наз. k-й стационарной Г. г. (стабильной Г. г.) сфер. Аналогичное явление стабилизации наблюдается для Г. г. ортогональных групп, Г. г. Тома пространств МSO и во многих других случаях. Общее изучение этого явления наиболее удобно проводить в рамках так наз. теории спектров. В этой теории стационарные Г. г. появляются как Г. г. спектров. Эти группы устроены существенно проще Г. г. пространства и их изучение (и вычисление) оказывается значительно более легкой задачей. Напр., для вычисления этих групп имеется специальный аппарат: спектральная последовательность Адамса.

Г. г. обобщались в самых различных направлениях. Напр., делались попытки заменить сферы другими пространствами. Здесь можно отметить торусные Г. г., позволившие проинтерпретировать Уайтхеда произведения как нек-рые коммутанты. Показано также, что в множество гомотопич. классов отображений X → Y тогда и только тогда можно ввести естественную по Y групповую операцию, когда X является ко-Н-пространством. Были определены Г. г. с коэффициентами, получающиеся при замене сфер Sⁿ Мура пространствами M(G, n). Это определение Г. г. с коэффициентами оказалось не очень удачным. Более удовлетворительное определение (согласующееся с общим принципом двойственности Экмана-Хилтона) было получено при замене M-пространств Мура ко-M-пространствами. Однако эти Г. г. определены не для всех G (напр., при G, являющейся аддитивной группой действительных чисел, эти группы не определены).

Детально изучен также вопрос о построении Г. г. в категориях, отличных от категории пунктированных пар. Здесь в первую очередь следует отметить построение Г. г. триад (см., напр., [3]), оказавшихся очень полезными при изучении гомоморфизма Е. Весьма общие конструкции Г. г. были предложены в связи с исследованиями по двойственности. На основе понятия стандартной конструкции (см. [6]) построение Г. г. было перенесено на произвольные категории. Существенную роль в этом построении играют уже упоминавшиеся Г. г. симплициальных множеств.

Лит.: [1] Стинрод Н., Топология косых произведений, пер. с англ., М., 1953; [2] Болтянский В. Г., Гомотопическая теория непрерывных отображений и векторных полей, М., 1955; [3] Xу Сы-цзян, Теория гомотопий, пер. с англ., М., 1964; [4] Браун Э. X., «Математика», 1958, т. 2:2, с. 3-24:. [5] Кан Д., там же, 1962, т. 6, № 1, с. 3-32; [6] Столлингс Дж., там же, 1964, 8:4, с. 155-57; [7] Экман Б., Хилтон П., там же, 1960, 4 : 3, с. 3-27; [8] Сулливан Д., Геометрическая топология, пер. с англ., М., 1975.

М. М. Постников.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.