ГОМОЛОГИЧЕСКИЕ УМНОЖЕНИЯ

ГОМОЛОГИЧЕСКИЕ УМНОЖЕНИЯ - операции, определенные на группах Тоr и Ext. Над коммутативным кольцом K рассматриваются K-алгебры R, S и T = R⊗_KS. Производные функторы Тоr и Ext над ними можно комбинировать между собой посредством четырех гомоморфизмов, наз. гомологическимиумножениям и:

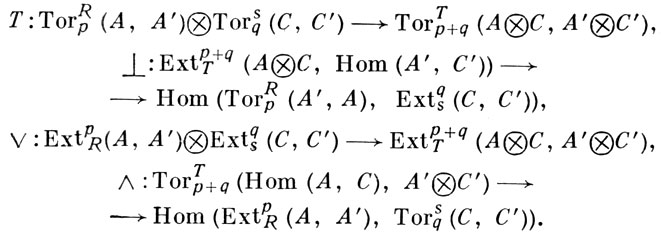
Здесь A и A' правые или левые A-модули, С и С' правые или левые S-модули, а символ K опущен при всех функторах. Последние два гомоморфизма определены только, если алгебры R и S проективны над K и Тоr^K_n(A, С) = 0 для всех n > 0. При нек-рых дополнительных ограничениях можно определить внутренние умножения, связывающие Тоr и Ext над одним и тем же кольцом.

Все четыре умножения могут быть получены из формул, переставляющих функторы ⊗ и Ноm с помощью замены аргументов соответствующими резольвентами (см. [1]). Умножение ∨ допускает следующую интерпретацию в терминах умножений Ионеда. Пусть

0 → А' → Х₁ → ... → X_p → А → 0,

0 → С → Y₁ → ... → Y_q → C → 0

- точные последовательности R- и S-модулей, соответственно, являющиеся представителями классов конгруэнтности в Ext^p_R(A, A') и Ехt^q_S(С, С'). Умножая первую из них тензорно справа на С', а вторую - слева на А, получают точные последовательности

0 → A'⊗С → Х₁⊗С' → ... → Х_p⊗С' → А⊗С' → 0,

→ А⊗С' → 0, 0 → A⊗C' → A⊗Y₁ → ... → A⊗Y_q → A⊗C → 0,

объединяемые в точную последовательность

0 → A'⊗С' → Х₁⊗С' → . .. → A⊗Y_q → А⊗С → 0.

к-рую можно рассматривать в качестве представителя класса конгруэнтности в группе

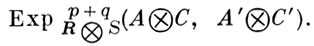
Умножение ∨ в когомологии H(Х, ℤ) топологич. пространства X с коэффициентами в кольце целых чисел ℤ носит название умножения Колмогорова-Александера или U-умножения.

Лит.: [1] Картан А., Эйленберг С., Гомологическая алгебра, пер. с англ., М., 1960; [2] Маклейн С., Гомология, пер. с англ., М., 1966.

В. Е. Говоров.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.