ГОМОЛОГИЧЕСКАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ

ГОМОЛОГИЧЕСКАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ - бесконечная в обе стороны точная последовательность гомологии трех комплексов, связанных короткой точной последовательностью. Пусть 0 → К. → L. → М. → 0 - точная последовательность цепных комплексов в абелевой категории. Тогда для любого n определены морфизмы гомологии

∂_n: Н_n(М.) → Н_n-1(К.),

наз. связывающими (или граничными) морфизмами. В категории модулей они определяются особенно просто: для h ∈ H_n(M.) выбирается прообраз х ∈ L_n; тогда dx является образом нек-рого элемента z ∈ Z_n-1(K.), класс гомологии к-рого есть ∂_n(h). Построенная с помощью связывающих морфизмов последовательность гомологии

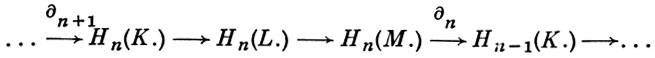
является точной и наз. гомологической последовательностью. Таким образом, гомологии являются гомологическим функтором на категории комплексов.

Двойственным образом определяется когомологическая последовательность.

Лит.: [1] Картан А., Эйленберг С., Гомологическая алгебра, пер. с англ., М., 1960.

В. И. Данилов.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.