ГОМОЛОГИЧЕСКАЯ АЛГЕБРА

ГОМОЛОГИЧЕСКАЯ АЛГЕБРА - раздел алгебры, основным объектом изучения к-рого являются производные функторы на различных категориях алгебраич. объектов (модулей над данным кольцом, пучков и т. д.).

Одним из истоков Г. а. явилась теория гомологии топологич. пространств, в к-рой каждому топологич. пространству X сопоставляется последовательность абелевых групп Н_n(Х) (групп гомологии), а непрерывному отображению f : X → Y пространств - набор гомоморфизмов f_n : H_n(Х) → H_n(Y) групп гомологии. Каждый n-мерный сингулярный симплекс Т топологич. пространства X имеет границу, состоящую из сингулярных симплексов размерности n-1. Если К_n - свободная абелева группа, порожденная всеми этими n-мерными симплексами, то функция ∂, к-рая сопоставляет каждому Т альтернированную сумму ∂Т его граничных симплексов, определяет гомоморфизм ∂ : K_n → K_n-1, так что

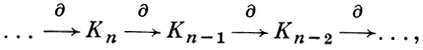
причем непрерывное отображение пространств индуцирует гомоморфизм соответствующих им комплексов. Некоторые свойства пространства X или отображения f : Х → Y могут быть найдены по свойствам группы H_n гомологии этого комплекса или соответствующих гомоморфизмов f_n этих групп гомологий, что в ряде случаев позволяет свести изучение топологич. объектов к изучению нек-рых алгебраич. объектов, подобно тому, как это делается в аналитич. геометрии (но с той разницей, что переход от геометрии к алгебре в теории гомологий необратим).

В свою очередь, в алгебре в связи с изучением расширений групп фактически рассматривались первая и вторая группы гомологий и когомологий. Значительный подготовительный материал был разработан в теории ассоциативных алгебр, алгебр Ли, теории конечномерных алгебр, теории колец, теории квадратичных форм.

В процессе изучения групп гомологий сложился прежде всего язык Г. а. Появились обозначения отображений с помощью стрелок и коммутативные диаграммы (если в графе отображений два пути, имеющие общие начало и конец, приводят к одному и тому же результату, то такую диаграмму наз. коммутативной). Часто встречались последовательности гомоморфизмов, в к-рых ядро исходящего гомоморфизма совпадало с образом входящего, такие последовательности назвали точными. Стало обычаем задавать математич. объекты одновременно с их отображениями, а наиболее предпочтительными считались соответствия между объектами, сохраняющие отображения, названные функторами. Основные достоинства этого языка - информативность, естественность и наглядность, быстро получили признание. Напр., в [5] язык Г. а. был использован для аксиоматич. изложения оснований алгебраич. топологии. В настоящее время язык Г. а. присутствует во многих работах, даже не использующих ее методов.

К середине 40-х гг. 20 в. Г. а. выделяется в самостоятельную область алгебры. Основная сфера применения Г. а.- категория модулей над кольцом. Большинство результатов, известных для модулей, переносится на абелевы категории с нек-рыми дополнительными ограничениями (это объясняется тем, что такие категории вкладываются в категорию модулей). Наиболее содержательное расширение области применения Г. а. было осуществлено в [4], где Г. а. была перенесена на произвольные абелевы категории с достаточным запасом инъективных объектов и стала приложимой к арифметической алгебраич. геометрии и теории функций многих переменных (см. Гротендика категория).

Основные функторы Г. а. - Ноm(A, В) (группа гомоморфизмов модуля A в модуль В) и тензорное произведение модулей A ⊗ В. Основа теории - изучение производных функторов, к-рые строятся, напр., следующим образом. Произвольный модуль А может быть представлен как фактормодуль свободного модуля F₀, затем рассматривается такое же представление F₁ для ядра предыдущего представления и т. д. В результате возникает точная последовательность

... → F_n → ... → F₁ → F₀ → A → 0.

Последовательность

... → P_n → ... → P₁ → P₀ → 0,

где все модули Р_i - проективны, наз. проективной резольвентой модуля А. Применение к ней ковариантного аддитивного функтора Т дает комплекс, группы гомологии к-рого наз. левыми производными функтора T и обозначаются L_nТ. Двойственно (для контравариантного функтора) или, используя инъективные модули и инъективные резольвенты (для ковариантного функтора), строятся правые производные функторы RⁿT. Производные функторы измеряют в нек-ром смысле отклонение функтора от точности. Они не зависят от произвола построения резольвенты. Каждой точной последовательности

0 → A → B → С → 0

соответствуют две бесконечные точные последовательности производных функторов:

... → L_n+1T(C) → L_nT(А) → L_nT(B) → L_nT(С) → L_n-1Т(С) → ... → R^n-1T(С) → RⁿТ(А) → RⁿT(В) → RⁿT(С) → Rⁿ⁺¹T(A) → ...

Для производных функторов основных функторов приняты следующие обозначения:

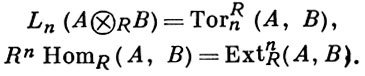
Оба эти функтора являются функторами двух аргументов А и В, поэтому изложенная конструкция построения производного функтора к ним непосредственно неприменима. В данном случае можно фиксировать один из аргументов и строить резольвенту для другого или, взяв резольвенты для обоих аргументов, можно построить нек-рый двойной комплекс. Все эти построения приводят к одному и тому же результату. Группа Ext¹_R(A, В) изоморфна группе расширений модуля В с помощью модуля А (и в этом виде давно изучалась). Установление новых связей значительно расширило и продвинуло теорию расширений модулей. Группа Tor^R₁(A, O/ℤ) сопоставляет каждой группе А ее периодич. часть. Обобщение этого наблюдения привело к общей теории кручения.

В общую схему производных функторов укладывается теория гомологии алгебраич. систем. Напр., пусть Λ = ℤG - групповое кольцо мультипликативной группы G над кольцом ℤ целых чисел, А - левый, а В - правый Λ-модули. Изучение групп

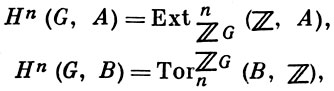
где ℤ рассматривается как тривиальный левый ℤG-мoдуль, составляет теорию гомологии и когомологий групп. Пусть L - алгебра Ли над полем k, UL - ее универсальная обертывающая алгебра, А есть UL-модуль. Изучение групп

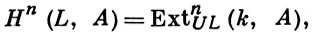
где k рассматривается как тривиальный UL-модуль, составляет теорию когомологий алгебр Ли. Аналогично определяются подходящие группы когомологий и гомологий моноидов, абелевых групп, алгебр, градуированных алгебр, колец и т. д. Руководящей идеей в каждом случае служит то, что вторая группа когомологий представляет группу расширений для рассматриваемого типа алгебраич. систем.

В свою очередь, гомологии алгебраич. систем являются предметом изучения относительной гомологической алгебры.

В конкретных случаях вычисление производных функторов обычно достигается с помощью удачно построенной резольвенты. Иногда резольвента оказывается конечной (напр., длина резольвенты произвольной абелевой группы не превосходит 1). Существует давний и вполне оправданный интерес к длине самой короткой резольвенты (эта длина наз. гомологической размерностью). Первый значительный результат в этом направлении - Гильберта теорема о сизигиях (конец 19 в.). Теория гомологич. размерности - одна из активно развивающихся ветвей Г. а. Переход от модулей с различными ограничениями конечности к общему случаю часто осуществляется с помощью функторов индуктивных пределов (lim_→) и проективных пределов (lim_←). Напр., всякая группа является индуктивным пределом своих конечно порожденных подгрупп. Всякая компактная вполне несвязная группа представима в виде проективного предела своих конечных факторгрупп. Интерес к этим группам вызван их связями с теорией Галуа. Производные этих функторов применяются в теории гомологич. размерности.

Изучаются производные функторы для неаддитивных функторов (напр., функтора, сопоставляющего абелевой группе ее групповое кольцо или симметрическую алгебру).

К основным средствам вычисления Г. а., кроме уже отмеченных резольвент, следует отнести спектральные последовательности и гомологические умножения. Спектральные последовательности, являясь наиболее мощным аппаратом исследования производных функторов, аппроксимируют группы гомологии группы группами гомологии ее подгруппы и факторгруппы. Гомологич. умножения изучают, гомоморфизмы типа

L_nT ⊕ L_mT → L_m+nT,

комбинирующие между собой производные функторы.

Методы Г. а. широко используются в настоящее время в самых различных разделах математики - в функциональном анализе, теории функций комплексного переменного, дифференциальных уравнениях и др. Без Г. а. немыслимы такие разделы алгебры, как алгебраич. К-теория, алгебраич. геометрия, алгебраич. теория чисел.

Лит.: [1] Картан А., Эйленберг С., Гомологическая алгебра, пер. с англ., М., 1960; [2] Маклейн С., Гомология, пер. с англ., М., 1966; [3] Басе X., Алгебраическая K-теория, пер. с англ., М., 1973; [4] Гротендик А., О некоторых вопросах гомологической алгебры, пер. с франц., М., 1961; [5] Стинрод Н., Эйленберг С., Основания алгебраической топологии, пер. с англ., М., 1958; [6] Итоги науки. Сер. Математика. Алгебра. 1964, М., 1966, с. 203-36; [7] Steenrod N. Е., Reviews of papers in algebraic and differential topology, topological and homological algebra, pt. 2, Princeton, p. 1174-364.

В. E. Говоров, А. В. Михалев.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.