ГОМОЛОГИИ ТЕОРИЯ

ГОМОЛОГИИ ТЕОРИЯ топологических пространств - часть алгебраич. топологии, осуществляющая связь между топологич. и алгебраич. понятиями: приводя в соответствие каждому пространству определенную последовательность групп, а непрерывному отображению пространств - гомоморфизмы соответствующих групп, Г. т. по свойствам групп и их гомоморфизмов позволяет судить о свойствах пространств и отображений. К таким свойствам относятся, напр., связности разлинных размерностей, для исследования к-рых Г. т. опирается на понятие ограничивания, в отличие от другой части алгебраич. топологии - теории гомотопии, к-рая для той же цели применяет деформации. Г. т. зародилась в конце 19 в. в трудах А. Пуанкаре (Н. Poincaré) (см. Гомологии полиэдра), но аксиоматич. построение (а вместе с ним и точные границы этого долгое время расплывчатого понятия) Г. т. полупила лишь в работах Н. Стинрода и С. Эйленберга (см. [3], а также Алгебраическая топология, Гомологии группа, Стинрода-Эйленберга аксиомы).

По этому построению теория гомологии {Н, ∂} есть совокупность трех функций: 1) относительной r-мерной группы гомологии Н_r(Х, А) пары топологич. пространств (X, A), A ⊂ X, к-рая каждой паре (X, А) и каждому целому числу r ставит в соответствие абелеву группу Н_r(Х, А); 2) гомоморфизма

H_r(f) = f_*: H_r(X, А) → Н_r(Y, В),

к-рый ставится в соответствие непрерывному отображению f: (X, A) → (Y, В) и числу r и наз. гомоморфизмом, индуцированным отображением f; 3) граничного оператора ∂, к-рый каждой паре (X, А) и каждому r ставит в соответствие гомоморфизм ∂ группы Н_r(Х, А) в группу H_r-1(A) (так наз. абсолютную группу пространства А, являющуюся группой пары (А, ∅)). При этом указанные функции должны удовлетворять следующим аксиомам.

1. Если f - тождественное отображение, то таковым является и f_*.

2. (gf)_* = g_*f_*.

3. ∂f_* = (f|A)_*∂.

4. Аксиома точности. Если

i : A → Х и j : Х → (Х, А)

- отображения вложения, то последовательность

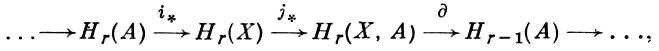
наз. гомологической последовательностью, пары (X, А), является точной последовательностью, т. е. везде образ входящего гомоморфизма совпадает с ядром исходящего.

5. Аксиома гомотопии. Если отображения

f, g : (X, A) → (Y, В)

гомотопны, то f_* = g_*.

6. Аксиома вырезания. Если U - открытое подмножество пространства X и его замыкание содержится во внутренности подпространства А, то отображение вложения

e : (X\U, A\U) → (X, А)

индуцирует изоморфизм е_*.

7. Аксиома размерности. Если X - одноточечное пространство, то Е_r(Х) = 0 для всех r ≠ 0.

Вместо категории всех пар пространств за область определения функции Н_r можно взять произвольную категорию пар пространств, напр. категорию пар компактных пространств или категорию пар, состоящих из полиэдров и их подполиэдров. Однако требуется, чтобы такая категория вместе с (X, А) содержала пары (∅, ∅), (X, ∅) = Х, (А, ∅) = А, (А, А), (X, X), цилиндр (X, А) × I, I = [0, 1], и какое-либо одноточечное пространство Р₀, со всеми их отображениями вложения. Кроме того, требуется, чтобы категория содержала все пары и отображения, к-рые встречаются в аксиомах или теоремах. С другой стороны, за область значений функции Н_r вместо категории всех абелевых групп можно принимать и другие категории, напр. категорию топологических, в частности, компактных групп с непрерывными гомоморфизмами или категорию модулей над нек-рым кольцом с линейными гомоморфизмами.

Аксиомы 1 и 2 означают, что Н_r есть ковариантный функтор из нек-рой категории пар пространств в категорию групп. Аксиома 3 означает, что граничный оператор д согласован с функтором Н_r. Аксиома 4, связывающая функторы всех размерностей r, иногда заменяется более слабым требованием: чтобы последовательность была лишь полуточной, т. е. образ входил в ядро (см. Точная последовательность); важным примером частично полуточной теории гомологии является теория гомологии Александрова-Чеха. Аксиома 5 имеет эквивалентную форму: если

f₀f₁ : (X, А) → (Х, А) × I

- отображения, определяемые формулами f₀(x) = (x, 0), f₁(x) = (x, 1), то f_0* = f_1*. Аксиома 6, требующая инвариантность при вырезании и имеющая несколько разновидностей, указывает то свойство Г. т., к-рое отличает ее от теории гомотопий. Аксиома 7, обеспечивающая геометрич. значимость размерностного индекса r, в современных исследованиях часто пренебрегается, что порождает так наз. обобщенные теории гомологии, важным примером к-рых служит теория бордизмов.

Для Г. т. существует двойственная ей теория когомологий (см. Двойственность в топологии). Она задается: относительной r-мерной группой когомологий Н^r(Х, А), являющейся контравариантным функтором из категории пар топологич. пространств в категорию абелевых групп с индуцированным гомоморфизмом

Н^r(f) = f^*: H^r(Y, В) → Н^r(Х, А)

и кограничным оператором

δ: Н^r(А) → Н^r+1(Х, А).

Аксиомы формулируются так же, как и в случае гомологии, с очевидным изменением в направлении гомоморфизмов, происходящим от контравариантности; напр., аксиома точности требует, чтобы была точной когомологическая последовательность

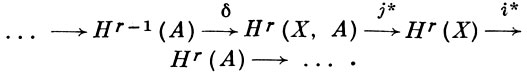
Здесь возникают также обобщенные когомологич. теории, важными примерами к-рых служат К-теории и кобордизмы. Приводимые ниже факты Г. т. имеют когомологич. параллели.

Группой коэффициентов Г. т. или теории когомологий наз. группа H₀(Р₀) или соответственно Н⁰(Р₀). Группы Н̃_r(Х, А) иногда удобно заменять так наз. приведенными группами Н̃_r(X, А): приведенная нульмерная группа гомологии Н₀(Х) есть ядро гомоморфизма

l_* : Н₀(X) → Н₀(Р₀),

индуцированного отображением l : Х → Р₀, а приведенная нульмерная группа когомологий H̃⁰(Х) есть факторгруппа группы Н⁰(Х) по образу f^*(H⁰(P₀)); приведенные группы других размерностей совпадают с исходными: Н̃_r(Х) = Н_r(Х), r ≠ 0. Так, H₀(Х) ~ H̃₀(X) ⊕ G. Если А ≠ ∅, то H̃_r(X, A) = H_r(X, А) при всех r. Замена обычных групп приведенными позволяет получить из гомологич. последовательности приведенную гомологическую последовательность.

Аксиомы Г. т. не являются независимыми. Так, аксиома 1 есть следствие аксиом 2, 3, 4. Система аксиом совместна, как показывает пример тривиальной теории Н_r(Х, А) = 0; нетривиальными примерами являются когомологич. теория Александрова-Чеха, сингулярные гомологии и др. В вопросе полноты имеет место следующее: гомоморфизмом Г. т. {H, ∂} в Г. т. {H', ∂'} наз. такая система гомоморфизмов

h(X, А; r) : Н_r(Х, А) → Н'_r(Х, А),

что

H'(f) ⋅ h(X, A; r) = h(Y, В; r) ⋅ H(f)

и

∂' ⋅ h(X, A; r) = h(A; r-1) ⋅ ∂;

если все h(X, А; r) - изоморфизмы, то Г. т. {H, ∂} и {H', ∂'} наз. изоморфными Г. т. На конечных полиэдрах Г. т. является единственной. Точнее, если h₀ : G → G' - произвольный гомоморфизм группы коэффициентов G теории {H, ∂} в группу коэффициентов G' теории {H', ∂'}, то для каждой полиэдральной пары (X, А) существует единственный гомоморфизм

h(X, А; r) : Н_r(Х, А) → Н_r(Х, А),

обладающий тем свойством, что h(P₀; 0) = h₀, причем, если h₀ - изоморфизм, то изоморфизмами являются и все h(X, А; r). Так как группы гомологии отрицательной размерности триангулируемой пары тривиальны, то для таких пар равенство H_r(Х, A) = 0̇, r < 0, имеет место и при любой Г. т. {H, ∂}. Теорема единственности справедлива и для более широких категорий пространств в случае, когда Г. т. удовлетворяет соответствующим дополнительным аксиомам.

Группы гомологии являются топологическими, а также гомотопич. инвариантами: если f есть гомотопич. эквивалентность, то есть изоморфизм. Если X -стягиваемое пространство, в частности, клетка, то H_r(Х) = 0, r ≠ 0, и H₀(X) ~ G. Если i : A ⊂ X есть гомотопич. эквивалентность, то H_r(Х, А) = 0, и, при любом X, Н_r(Х, Х) = 0. Если А - ретракт пространства X, то i_* есть мономорфизм, j_* - эпиморфизм, оператор ∂ тривиален и

H_r(Х) ~ H_r(A) ⊕ H_r(X, А).

Если X деформируемо в А, то i_* есть эпиморфизм, j_* тривиален, ∂ есть мономорфизм и

H_r(A) ~ H_r(X) ⊕ H_r+1(X, А).

Пусть через S(X) обозначена надстройка над X; имеет место изоморфизм

H̃_r(X) ~ H_r+1(S(X)).

Это дает возможность вычислить группы гомологии сфер Sⁿ; именно: H̃_r(Sⁿ) = 0 при r ≠ n и H̃_n(Sⁿ) ~ G; следовательно, H_r(Sⁿ) = 0 при n ≠ r ≠ 0, H_r(Sⁿ) ~ G при n ≠ r = 0 или n = r ≠ 0 и H₀(S⁰) ~ G ⊕ G.

Важную роль в Г. т. играют гомологические последовательности троек и триад. Для тройки (X, А, В), X ⊃ A ⊃ B, пространств граничный оператор ∂' = k*∂ определяется как композиция k'_* ⋅ ∂, где k': А → (A, В) есть вложение. Тогда возникает так наз. гомологическая последовательность тройки (X, А, В) (сводящаяся при B = ∅ к гомологич. последовательности пары (X, А))

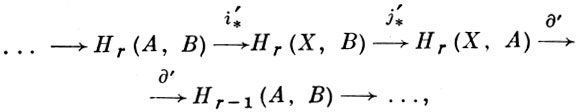
где i' : (А, В) → (Х, В) и j' : (X, B) → (Х, А) - вложения. Эта последовательность точна. Если группы Н_r(Х, А), Н_r(Х, В), Н_r(А, В) тривиальны для всех r, то i'_*, ∂', j'_*, являются соответственно изоморфизмами, и наоборот. Если X есть объединение непересекающихся замкнутых множеств X_i, i = 1, ..., n, и А = A₁ ∪ ... ∪ A_n, где A_i ⊂ X_i, то Н_r(Х, А) изоморфна прямой сумме групп H_r(Х_i, A_i), i = 1, ..., n. Триада (X; A, В) есть пространство X с упорядоченной парой А, В подпространств. Она является собственной триадой, если вложения

k: (А, А ∩ В) → (А ∪ В, В), l: (В, А ∩ В) → (А ∪ В, А)

индуцируют изоморфизмы или имеется разложение

H_r(A ∪ B, A ∩ B) ~ H_r(A, A ∩ B) ⊕ H_r(B, А ∩ В).

Далее, для них определяется граничный оператор

∂̅ : Н_r(Х, A ∪ B) → H_r-1(A, A ∩ B)

как k^-1_* ⋅ m_* ⋅ ∂, где m : A ∪ B ⊂ (A ∪ B, В). Это порождает точную гомологическую последовательность триады

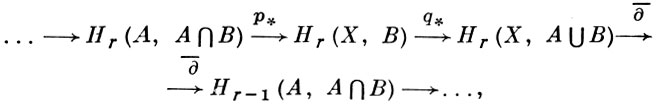
где р : (А, А ∩ B) → (Х, В), q : (X, B) → (Х, A ∪ B) -вложения [при В ⊂ А эта последовательность сводится к гомологич. последовательности тройки (X, А, В)).

Пусть Х = A ∪ B, A ∩ B = C и пусть для отображений h, h₁, h₂ : (X, С) → (Y, D) имеют место соотношения h₁|A = h|A, h₂|B = h|B, h₁(B) ⊂ D, h₂(A) ⊂ D. Тогда справедливы следующие аддиционные теоремы.

1. h_* = h_1* + h_2*.

2. Если D стягиваемо и f, f₁, f₂ : X → Y определены соответственно посредством h, h₁, h₂, то для индуцированных гомоморфизмов приведенных групп f_*, f_1*, f_2* : H̃_r(Х) → H_r(Y) имеет место равенство f_* = f_1* + f_2*.

Пусть определен гомоморфизм

s : H_r(C) → H_r(A) ⊕ H_r(В),

где s(c) = (s_1*(c), - s_2*(c)), с ∈ Н_r(С) и где s₁ : C → A, s₂ : С → В - вложения, и гомоморфизм

t : H_r(A) #&8853; H_r(B) → H_r(X),

где t(a, b) = t_1*(a) + t_2*(b), (а, b) ∈ Н_r(A) ⊕ H_r(В), и t₁ : А → Х, t₂ : B → Х - вложения. Пусть, наконец, определен гомоморфизм

Δ : H_r(Х) → Н_r(С),

где Δ = du^-1_*1v_* и

v : X → (X, В), u : (А, С) → (X, В)

- вложения. Тогда получается так наз. последовательность Мейера-Вьеториса собственной триады:

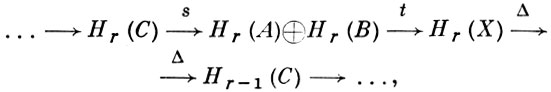
к-рая является точной и к-рая связывает гомологии пространств с гомологиями их объединения и пересечения. Отсюда, в случае С ≠ ∅, можно перейти к аналогичной последовательности для приведенных групп. Из нее следует:

1. Если A ∩ B стягиваемо, то

Н̃_r(А ∪ В) ~ Н̃_r(А) ⊕ H̃_r(В).

2. Если A ∪ В стягиваемо, то

H̃_r(A ∪ B) ~ H̃_r(A) ⊕ H̃_r(B).

3. Если А и В стягиваемы, то Δ устанавливает изоморфизм

Н̃_r(А ∪В) ~ Н̃_r-1(А ∩ В).

Использование предыдущих результатов позволяет вычислить группы гомологии различных пространств. Напр., если X - замкнутая ориентируемая поверхность рода n, то H_r(Х) изоморфна группе коэффициентов G при r = 0, 2, прямой сумме G²ⁿ 2n экземпляров группы G при r = 1 и 0 - в остальных случаях. Если X - замкнутая неориентируемая поверхность рода n, то H_r(Х) изоморфна G при r = 0, группе G^n-1 ⊕ G₂, где G₂ есть факторгруппа G/2G, 2G = {2g| g ∈ G}, при r = 1, подгруппе T₂(G) группы G, состоящей из всех элементов g ∈ G с 2g = 0 при r = 2 и 0 - в остальных случаях. Таким образом, Г. т. дает топологич. классификацию замкнутых поверхностей. Для n-мерного действительного проективного пространства Рⁿ группа H_r(Рⁿ) изоморфна группе G при r = 0 или r = n и нечетном, группе G₂ при r нечетном и 0 < r < n, группе T₂(G) при r четном и 0< r ≤ n и 0 - в остальных случаях. Группа гомологии H_r(СРⁿ) комплексного проективного пространства СРⁿ размерности 2n изоморфна группе G при r четном и 0 ≤ r ≤ 2n и 0 - в остальных случаях. Гомологич. группа H_r(L_p,q) линзового пространства L_p,q изоморфна группе G при r = 0,3, группе G_p =G/pG, гд'е pG = {pg| g ∈ G} при r = 1, группе T_p(G), где T_p(G) = {g ∈ G| pg=0} при r = 2 и 0 - в остальных случаях.

Из разнообразных приложений предыдущих результатов следует выделить нек-рые фундаментальные предложения. Прежде всего - инвариантность размерности: сферы, а также евклидовы пространства различных размерностей не гомеоморфны; более того, если два полиэдра гомеоморфны, то они имеют одинаковую размерность. Далее, из равенства f_*i_* = g_*, где f : X → Y есть распространение данного отображения g : A → Y, A ⊂ Х, получаются различные признаки распространяемости и ретрагируемости отображений; напр., отображение ненулевой степени сферы S^n-1, n > 1, в себя не распространимо на n-мерный шар Еⁿ, границей к-рого является S^n-1, а сфера S^n-1 не является ретрактом шара Еⁿ ни для какого натурального n. Из этого, в свою очередь, следует теорема Брауэра о неподвижной точке: любое отображение Еⁿ → Еⁿ имеет неподвижную точку. Наконец, доказывается, что на Sⁿ существует единичное касательное векторное поле тогда и только тогда, когда n нечетно, а из теории триад получается ряд теорем о степенях отображений, что, в частности, позволяет по-новому доказать основную теорему алгебры.

Лит.: [1] Александров П. С., Комбинаторная топология, М.-Л., 1947; [2] Лефшец С., Алгебраическая топология, пер. с англ., М., 1949; [3] Стинрод Н., Эйленберг С., Основания алгебраической топологии, пер. с англ., М., 1958; [4] Спеньер Э., Алгебраическая топология, пер. с англ., М., 1971; [5] Нu Sze-Tsen, Homology Theory; 3 ed., N.-L., 1965; [6] Ни Sz.-Tz., Cohomology Theory, L., 1970; [7] Дольд А., Лекции по алгебраической топологии, пер. с англ., М., 1976.

Г. С. Чогошвили.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.