ГОМЕОМОРФИЗМОВ ГРУППА

ГОМЕОМОРФИЗМОВ ГРУППА - группа 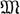(X) гомеоморфных отображений топологич. пространства X на себя. Если X - компактное многообразие, то алгебраич. свойства группы 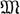(X), а именно, структура ее нормальных делителей, определяют X с точностью до гомеоморфизма (см. [1]). В частности, при n ≠ 4 известно, что группа 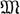(Sⁿ) есть простая группа. Это верно также для канторова множества, кривой Менгера, кривой Серпинского, множеств рациональных и иррациональных точек на прямой [2]. Для многообразия М минимальным нормальным делителем в 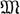(М) служит подгруппа, порожденная гомеоморфизмами, тождественными вне областей М.

Группа 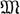(X) может быть топологизирована различным образом (см. Пространства отображений). Основное значение имеют бикомпактно открытая топология и (если X метризуемо) тонкая С⁰-топология, в к-рой окрестности тождества О_f задаются строго положительными функциями f : X → -(0, ∞), причем h ∈ 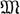(X) входит в О_f, если ρ(hx, x) < f(x) для всех х, где ρ - метрика в X. Однако группа 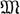(X) не обязана быть топологической группой в этих топологиях, так как отображение h → h^-1 не всегда непрерывно, и даже если это так, то 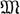(X) может не быть топологич. группой преобразований, т. е. отображение (h, x) → hx может быть разрывным (см. [3]). Но если X - многообразие, то 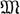(X) является топология, группой преобразований в обеих указанных топологиях. Изучение топологич. свойств группы 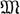(X) представляет интерес, в первую очередь, для однородного пространства X, т. е. такого, что действие группы 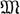(Х) на X транзитивно. Однако такое изучение проведено далеко не полностью даже для простых многообразий. Неизвестно, напр. (к 1977), будет ли 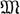(X) бесконечномерным многообразием, хотя оно будет (для метризуемого многообразия) локально стягиваемым в тонкой С⁰-топологии (см. [4]). В частности, два достаточно близких гомеоморфизма соединимы изотопией. Для открытых многообразий, к-рые являются внутренностью компактных многообразий, это верно также и в бикомпактно открытой топологии.

Факторгруппа Г(X) группы 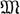(X) по компоненте тождества 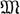₀(Х) наз. группой гомеотопий пространства X. Вообще говоря, 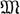₀(X) не совпадает с Г. г., гомотопных тождеству, но это так для двумерных и нек-рых трехмерных многообразий (напр., для S³, S² × S¹ и др.). Гомотопич. свойства 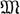₀ изучены для двумерных многообразий, что оказалось полезным для установления гомологич. свойств групп кос (см. Кос теория).

Особое значение в топологии многообразий имеет изучение нек-рых подгрупп группы 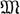(ℝⁿ), напр. подгруппы диффеоморфизмов. Это изучение затруднено тем, что подгруппы оказываются незамкнутыми, и топология факторпространств неудовлетворительна. Ввиду этого рассматривают полусимплициальные группы (ss-группы) Тор_n, в к-рых k-мерными симплексами служат послойные гомеоморфизмы Δ_k × ℝ_n, неподвижные на нулевом сечении (где Δ_k - стандартный k-симплекс). Граничные гомеоморфизмы и вырождения определяются с помощью стандартных отображений Δ^l × ℝⁿ → Δ^l × ℝⁿ. Аналогично определяются ss-моноид G_n ss-группы PL_n, Diff_n, O_n(гомотопич. эквивалентностей S^n-1 кусочно линейных, гладких и ортогональных отображений ℝⁿ), причем

G_n ⊃ Тор_n ⊃ PL_n ⊃ Diff_n ⊃ O_n,

и факторы G_n/Top_n и т. д. обладают естественными структурами ss-комплексов, что позволяет проводить изучение гомотопич. свойств этих вложений.

Изучение различных подгрупп 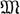(М) для многообразий М составляет предмет ряда дисциплин. В частности, изучение Г. г., сохраняющих определенные структуры, относится к соответствующим разделам математики. Большой интерес представляют алгебраич. задачи, связанные с группами автоморфизмов деревьев и других графов.

Лит.: [1] Whittaker J. V., «Аnn. Math.», 1963, v. 78, №1, p. 74-91; [2] Anderson R. D., «Аmеr. J. Math.», 1958, v. 80, № 4, p. 955-63; [3] Arens R. F., «Аmеr. J. Math.», 1946, v. 68, № 4, p. 593-610; [4] Чepнавский А. В., «Матем. сб.», 1969, т. 79, № 3, с. 307-56.

А. В. Чернавский.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.