ГОЛУБЕВА-ПРИВАЛОВА ТЕОРЕМА

ГОЛУБЕВА-ПРИВАЛОВА ТЕОРЕМА: если f(z) - комплексная суммируемая функция на замкнутой спрямляемой жордановой кривой L, расположенной в плоскости комплексного переменного z, то для существования регулярной во внутренней области D, ограниченной кривой L, функции F(z), угловые граничные значения к-рой совпадают с f(z) почти всюду на L, необходимо и достаточно, чтобы

∫_L zⁿf(z)dz = 0, n = 0, 1, 2, ... . (1)

Эти условия наз. условиями Голубева-Привалова. В. В. Голубевым [1] доказана их достаточность, а И. И. Приваловым [2] - необходимость. Иначе говоря, условия (1) необходимы и достаточны для того, чтобы интеграл типа Коши-Лебега (см. Коши интеграл) F(z), построенный для функции f(z) и кривой L:

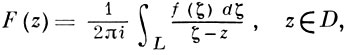
обращался в интеграл Коши-Лебега.

В более общей постановке, пусть μ - комплексная борелевская мера на L. Тогда, для того чтобы интеграл типа Коши-Стилтьеса

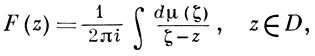
обращался в интеграл Коши-Стилтьеса, необходимо и достаточно, чтобы выполнялись обобщенные условия Голубева-Привалова

∫ zⁿ dμ(z) = 0, n = 0, 1, 2, ... . (2)

Иначе говоря, условия (2) необходимы и достаточны для существования регулярной в D функции P(z) такой, что ее угловые граничные значения почти всюду по мере Лебега на L совпадают с

е^-iφ(z)μ'(z),

где φ(z) - угол между положительным направлением оси абсцисс и касательной к L в точке z ∈ L, μ'(z) -производная меры μ по мере Лебега s (длина дуги) на L. Г.-П. т. имеет важное значение в теории граничных свойств аналитических функций.

Лит.: [1] Голубев В. В., Однозначные аналитические функции с совершенным множеством особых точек, М., 1916 (см. также его кн.: Однозначные аналитические функции. Автоморфные функции, М., 1961); [2] Привалов И. И., Интеграл Cauchy, Саратов, 1918; [3] его же, Граничные свойства аналитических функций, 2 изд., М.-Л., 1950.

Е. Д. Соломенцев.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.