ГОЛОМОРФНОСТИ ОБЛАСТЬ

ГОЛОМОРФНОСТИ ОБЛАСТЬ - область D комплексного пространства ℂⁿ, для к-рой существует функция f(z), голоморфная в D и не продолжаемая голоморфно в большую область; при этом D наз. естественной областью определения функции f(z). Напр., естественной областью определения функции

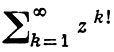
служит единичный круг, к-рый поэтому является Г. о. в ℂ¹. В ℂ¹ всякая область есть Г. о. Напротив, в ℂ¹, n ≥ 2, не всякая область есть Г. о. Так, никакая область вида D\K, где К - компакт, содержащийся в D, не будет Г. о.

Область D ⊂ ℂⁿ наз. голоморфно выпуклой, если для каждого множества A ⋐ D существует такое содержащее А множество F_A ⋐ D, что для любой точки z₀ ∈ D\F_A существует функция f(z), голоморфная в D и такая, что

sup_z∈A |f(z)| < |f(z₀)|.

Для того чтобы область D была Г. о., необходимо и достаточно, чтобы она была голоморфно выпуклой (теорема Картана-Туллена). Для того чтобы область D была Г. о., необходимо и достаточно, чтобы для каждой точки z₀ ∈ ∂D существовал барьер-функция f_z0(z), голоморфная в D и не продолжимая голоморфно в точку z₀. Напр., если D - произвольная область в ℂⁿ, то функция (z - z₀)^-1 есть барьер в любой точке z₀ ∈ ∂D, так что D есть Г. о.; если D - выпуклая область в ℂⁿ и

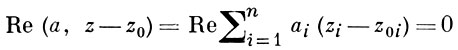
- опорная плоскость в точке z₀ ∈ ∂D, то функция (a, z - z₀)^-1 есть барьер в z₀, и поэтому всякая выпуклая область в ℂⁿ есть Г. о.

Пересечение Г. о. есть Г. о.; всякое биголоморфное отображение переводит Г. о. в Г. о.; сумма возрастающей последовательности Г. о. есть Г. о. (теорема Венке-Штейна).

Область D ⊂ ℂⁿ наз. псевдовыпуклой, если функция - ln Δ_D(z) есть плюрисубгармоническая функция в D, где Δ_D(z) есть расстояние от точки z ∈ D до ∂D. Для того чтобы область была Г. о., необходимо и достаточно, чтобы она была псевдовыпуклой (теорема Ока). Достаточность условия в теореме Ока составляет содержание проблемы Леви, поставленной Э. Леви (Е. Levi, в 1911). Для n = 2 она была решена К. Ока (К. Ока, 1942); для n ≥ 2 эта проблема решена независимо К. Ока, Ф. Норгэ, Г. Бремерманом (F. Norguet, Н. Bremermann, 1953-1954).

Г. о. с достаточно гладкой границей допускают локальное описание. Область D ⊂ ℂⁿ наз. псевдовыпуклой в точке z₀ ∈ ∂D, если существует такая окрестность V точки z₀ и такая определенная в V действительная функция φ(z) класса ℂ², что: a) D ∩ V = [z : φ(z) < 0, z ∈ V] и б) на плоскости

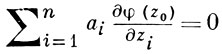
форма Гессе

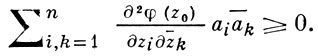
Если в условии б) имеет место строгое неравенство для всех рассматриваемых векторов а ≠ 0, то область D наз. строго псевдовыпуклой в точке z₀. Область D наз. (строго) псевдовыпуклой в смысле Леви, если она (строго) псевдовыпукла в каждой точке z₀ ∈ ∂D.

Если область строго псевдовыпукла в смысле Леви, то она псевдовыпукла (теорема Леви).

Г. о. функции f(z), заданной в первоначальной окрестности V, может быть построена при помощи разложений в ряды Тейлора с использованием принципа голоморфного продолжения; при этом может оказаться, что в построенной области голоморфно продолженная функция f(z) неоднозначна. Чтобы сделать функцию однозначной, необходимо расширить понятие области. Это достигается путем введения римановых областей (наложения областей, неоднолистных областей) над ℂⁿ (римановы области над ℂ¹ наз. римановыми поверхностями). Понятие Г. о. распространяется и на римановы области и даже на объекты более общей структуры - комплексные многообразия и комплексные пространства. Обобщение понятия Г. о. приводит к Штейна пространствам.

Лит.: [1] Владимиров В. С., Методы теории функций многих комплексных переменных, М., 1964; [2] Шабат Б. В., Введение в комплексный анализ, 2 изд., ч. 2, М., 1976; [3] Xёрмандер Л., Введение в теорию функций нескольких комплексных переменных, пер. с англ., М., 1968.

В. С. Владимиров.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.