ГОЛОМОРФНАЯ ФОРМА

ГОЛОМОРФНАЯ ФОРМА степени р на комплексном многообразии М - дифференциальная форма α типа (р, 0), удовлетворяющая условию d''α = 0, т. е. форма, к-рая в локальных координатах z₁, ..., z_n на М записывается в виде

α = ∑_i1,...,ip a_i1...ip dz^i₁ ∧ ... ∧ dz^p,

где a_i1...ip - голоморфные функции. Г. ф. степени р образуют векторное пространство Ω^p(М) над полем ℂ; Ω⁰(M) - это пространство голоморфных функций на М.

На компактном кэлеровом многообразии М пространство Ω^p(М) совпадает с пространством Н^p,0(М) гармонических форм типа (р, 0), откуда следует, что 2 dimΩ¹(М) есть первое число Бетти многообразия [1]. Г. ф. на римановой поверхности М наз. также дифференциалами первого рода; если поверхность М компактна, то dim Ω¹(М) равна ее роду.

Пространства Ω^p(M), р = 0, 1, ..., dim_ℂ M, образуют локально тонный комплекс относительно оператора d, наз. голоморфным комплексом де Рама. Если М - многообразие Штейна (см. Штейна пространство), то когомологий этого комплекса, изоморфны комплексным когомологиям Н^p(М, ℂ) и Н^p(М, ℂ) = 0 при p > dim_ℂM [2].

Аналогично определяются Г. ф. со значениями в нек-ром векторном аналитическом расслоении Е над М (голоморфные 0-формы здесь - голоморфные сечения расслоения). Ростки Г. ф. степени р со значениями в Е образуют локально свободный аналитич. пучок Ω^p_E. Комплекс Дольбо форм типа (р, q), q = 0, 1, ..., dim_ℂ M, со значениями в Е есть тонкая резольвента этого пучка, откуда

H^p,q(М, Е) ≅ Н^q(М, Ω^p_E)

(теорема Дольбо-Серра [1], [4]).

Определение Г. ф. можно распространить также на комплексные аналитич. пространства. Достаточно сделать это для локальных моделей, т. е. в случае, когда пространство А является аналитич. подпространством в области G ⊂ ℂⁿ. Пучок ростков голоморфных р-форм Ω^p_X на X определяется как

Ω^p_G/K^p|X,

где Ω^p_G - пучок ростков голоморфных р-форм в G, а К^p состоит из ростков форм вида

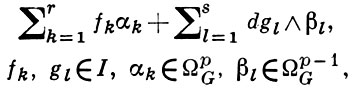
где I - пучок идеалов, задающий X. Определяется также голоморфный комплекс де Рама пространства X, к-рый, однако, не является локально тонным. Для того чтобы этот комплекс был локально точен в точке х ∈ Х, начиная с k-й степени, достаточно, чтобы X в окрестности точки х допускало голоморфное стягивание на локальное аналитич. множество Y ⊂ X, для к-рого emdim_xY = k (см. [3]).

Лит.: [1] Чжэнь Шэн-шэнь, Комплексные многообразия, пер. с англ., М., 1961; [2] Ганнинг Р., Росси X., Аналитические функции многих комплексных переменных, пер. с англ., М., 1969; [3] Reiffen H.-J., «Math. Z.», 1967, Bd 101, H. 4, S. 269-84; [4] Уэллс P., Дифференциальное исчисление на комплексных многообразиях, пер. с англ., М.. 1976.

А. Л. Онищик.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.