ГОДОГРАФА ПРЕОБРАЗОВАНИЕ

ГОДОГРАФА ПРЕОБРАЗОВАНИЕ - преобразование нек-рых дифференциальных уравнений математич. физики к линейному виду.

Бернулли интеграл и уравнение неразрывности плоскопараллельного потенциального установившегося движения баротропного газа (ρ = F(р))

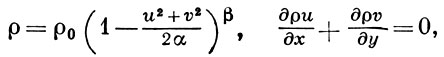
где

α = c²/(γ - 1) , β = 1/(γ - 1) (с -скорость звука для ρ = ρ₀)

приводят к уравнению

(*)

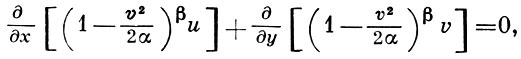
к-рое служит для определения потенциала скоростей

u = ∂φ/∂x, v = ∂φ/∂y

(u, v - компоненты скорости). Введением новых независимых переменных τ = v²/2α и θ, равной углу наклона вектора скорости к оси Ох, уравнение (*) приводится к линейному виду:

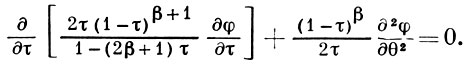
Это есть первое Г. п., или Чаплыгина преобразование. Второе Г. п. получается применением Лежандра преобразования прикосновения. В качестве новой неизвестной выбирается функция

Ф = x∂φ/∂x + y∂φ/∂y - φ

выраженная через u, v, к-рые вводятся вместо х, у как новые независимые переменные по формулам:

u = ∂φ/∂x, v = ∂φ/∂y.

Уравнение (*) принимает линейный вид:

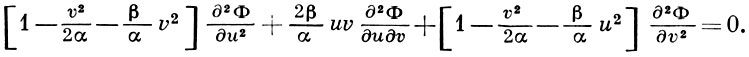
Г. п. применяются при решении задан теории струй и струйного обтекания криволинейных контуров газовым потоком.

Лит.: [1] Чаплыгин С. А., О газовых струях, М.-Л., 1949; [2] Кочин Н. Е., Кибель И. А., Розе Н. В., Теоретическая гидромеханика, 4 изд., М., 1963.

Л. Н. Сретенский.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.