ГЛУБИНА МОДУЛЯ

ГЛУБИНА МОДУЛЯ - одна из когомологич. характеристик модуля над коммутативным кольцом. Пусть А - нётерово кольцо, I - его идеал и пусть М есть А-модуль конечного типа. Тогда I-глубиной модулям наз. наименьшее целое число n, при к-ром

Extⁿ_A (A/I, М) ≠ 0.

Г. м. обозначают depth_I(M), или prof_I(M). Другое определение может быть дано в терминах M-регулярной последовательности, т. е. последовательности таких элементов a₁, ..., a_k из А, что а_i не является делителем нуля в модуле

M/(a₁, ..., a_i+1) М.

I-глубина модуля М равна длине наибольшей М-регулярной последовательности, составленной из элементов идеала I. В случае локального кольца А за I принимают обычно максимальный идеал. Верна следующая формула:

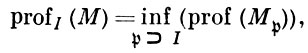
где ℘ означает простой идеал А, а М_℘ рассматривается как модуль над локальным кольцом А_℘.

Понятие Г. м. было введено в [1] под назв. гомологической коразмерности. Если проективная размерность dh(M) модуля М над локальным кольцом А конечна, то

dh(М) + prof(М) = prof(А).

В общем случае prof(M) не превосходит размерности модуля М.

Концепция Г. м. является одним из основных инструментов исследования модулей. Так, в терминах Г. м. определяются модули и кольца Коэна-Маколея; удобным часто оказывается условие Серра (S_k) на А-модуль M:

prof M_℘ ≤ inf (k, dim М_℘)

для всех простых идеалов ℘ в А. Наконец, Г. м. тесно связана с локальными когомологиями: утверждение

prof_I(М) ≥ n

равносильно тому, что модули локальных когомологий Нⁱ_I(М) равны нулю при i < n.

Лит.: [1] Auslander М., Buehsbaum D. А., «Рrос. Nat. Acad. Sci. USA», 1956, v. 42, p. 36-38; [2] Сepp Ж.-П., «Математика», 1963, т. 7, № 5, с. 3-93; [3] Grothendieck A., Cohomologie locale des faisceaux coherents, et theoremes de Lefschetz locaux et globaux, В., 1971.

В. И. Данилов.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.