ГЛОБАЛЬНАЯ СТРУКТУРА ТРАЕКТОРИЙ

ГЛОБАЛЬНАЯ СТРУКТУРА ТРАЕКТОРИЙ квадратичного дифференциала - описание поведения в целом траекторий положительного квадратичного дифференциала на конечной ориентированной римановой поверхности. Пусть R - конечная ориентированная риманова поверхность, Q(z)dz² - положительный квадратичный дифференциал на R; пусть С -множество всех нулей и простых полюсов Q(z)dz², а Н - множество всех полюсов Q(z)dz² порядка ≥2. Траектории Q(z)dz² образуют семейство F, обладающее многими свойствами регулярных семейств кривых. Это семейство кривых покрывает R, за исключением точек множества C ∪ H, т. е. через каждую точку из R\(С ∪ Н) проходит единственный элемент F. Поведение траекторий Q(z)dz² в окрестности любой точки R описывается локальной структурой траекторий квадратичного дифференциала. При рассмотрении глобальной структуры кривых семейства F в точках R\H существенную роль играют следующие объединения траекторий. Пусть Ф - объединение всех траекторий Q(z)dz², имеющих предельную концевую точку в нек-рой точке множества С; Λ - подмножество Ф, являющееся объединением всех траекторий Q(z)dz², к-рые имеют одну предельную концевую точку в точке множества С и вторую предельную концевую точку в точке множества С ∪ Н.

Множество K на R наз. F-множеством относительно Q(z)dz², если каждая траектория дифференциала Q(z)dz², пересекающаяся с K, полностью лежит в К. Внутреннее замыкание множества К определяется как внутренность замыкания K̅ и обозначается K̂. Внутреннее замыкание F-множества снова является F-множеством. Концевой областью Е относительно Q(z)dz² наз. наибольшее связное открытое F-множество на R, обладающее следующими свойствами: 1) Е не содержит точек множества C ∪ H; 2) Е заполнено траекториями дифференциала Q(z)dz², каждая из к-рых имеет предельную концевую точку в каждом из двух возможных направлений в данной точке А ∈ Н; 3) Е конформно отображается функцией

ζ = ∫[Q(z)]^1/2 dz

на верхнюю или нижнюю полуплоскость плоскости ζ (в зависимости от выбора ветви корня). Из локальной структуры траекторий Q(z)dz² следует, что точка А должна быть полюсом дифференциала Q(z)dz² не ниже 3-го порядка.

Полосообразной областью S относительно Q(z)dz² наз. наибольшее связное открытое F-множество на R, обладающее следующими свойствами: 1) S не содержит точек множества С ∪ Н; 2) S заполнено траекториями дифференциала Q(z)dz², каждая из к-рых имеет в одной точке А ∈ Н предельную концевую точку в одном направлении, а в другой (возможно, совпадающей с А) точке В ∈ Н - предельную концевую точку в другом направлении; 3) S конформно отображается функцией

ζ = ∫[Q(z)]^1/2dz

на полосу a < Im ζ < b, где а, b - конечные действительные числа, a < b. Точки А и В могут быть полюсами Q(z)dz² порядка 2 и более.

Круговой областью 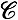относительно Q(z)dz² наз. наибольшее связное открытое F-множество на R, обладающее следующими свойствами: 1) 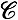содержит единственный двойной полюс А дифференциала Q(z)dz²; 2) 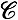\А заполнено траекториями дифференциала Q(z)dz², каждая из к-рых является замкнутой жордановой кривой, отделяющей А от границы 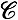; 3) при надлежащем выборе чисто мнимой постоянной с функция

w = exp { с ∫[Q(z)]^1/2 dz},

дополненная значением нуль в точке А, отображает 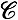конформно на круг |w| < R, причем точка А переходит в точку w = 0.

Кольцевой областью D относительно Q(z)dz² наз. наибольшее связное открытое F-множество на R, обладающее следующими свойствами: 1) D не содержит точек множества С ∪ Н; 2) D заполнено траекториями дифференциала Q(z)dz², каждая из к-рых является замкнутой жордановой кривой; 3) при надлежащем выборе чисто мнимой постоянной с функция

w = exp {с ∫[Q(z)]^1/2 dz}

отображает D конформно на круговое кольцо r₁ < |w| < r₂, 0 < r₁ < r₂.

Плотностной областью ℱ относительно Q(z)dz² наз. наибольшее связное открытое F-множество на R, обладающее свойствами: 1) ℱ не содержит точек множества Н; 2) ℱ\С заполнено траекториями Q(z)dz², каждая из к-рых всюду плотна в ℱ.

Справедлива основная структурная теорема (см. [2]). Пусть R - конечная ориентированная риманова поверхность, Q(z)dz² - положительный квадратичный дифференциал на R, причем исключаются следующие возможные случаи и все конфигурации, получающиеся из них посредством конформного отображения: I. R есть z-сфера, Q(z)dz² = dz²; II. R есть z-сфера, Q(z)dz² = Ke^iαdz/z², К - положительное, α -действительное числа; III. R есть тор, Q(z)dz² регулярен на R. Тогда: 1) R\Λ̅ состоит из конечного числа концевых, полосообразных, кольцевых, круговых и плотностных областей; 2) каждая такая область ограничена конечным числом траекторий вместе с точками, в к-рых последние встречаются; каждая граничная компонента такой области содержит точку множества С, за исключением граничных компонент круговой или кольцевой области, к-рые могут совпадать с граничными компонентами R; для полосообразной области два граничных элемента, выходящие из точек множества Н, разделяют границу на две части, на каждой из к-рых имеется точка множества С; 3) каждый полюс Q(z)dz² порядка m > 2 имеет окрестность, покрываемую внутренним замыканием объединения m - 2 концевых областей и конечного числа (возможно, равного нулю) полосообразных областей; 4) каждый полюс Q(z)dz² порядка m = 2 имеет окрестность, покрываемую внутренним замыканием объединения конечного числа полосообразных областей, или окрестность, содержащуюся в круговой области.

Из этой теоремы непосредственно следует утверждение основной структурной теоремы Дж. Дженкинса (J. Jenkins) в первоначальной формулировке (см. [1]): в условиях сформулированной теоремы множество R\Ф̅ состоит из конечного числа концевых, полосообразных, круговых и кольцевых областей. Большое внимание в ряде исследований теории однолистных функций уделяется доказательству того факта, что для рассматриваемого квадратичного дифференциала Q(z)dz² множество Ф̂ пусто. Нахождение условий, обеспечивающих пустоту множества Ф̂, представляет и самостоятельный интерес. Пример квадратичного дифференциала Q(z)dz² на z-сфере, для к-рого множество Ф̅ пусто, дает следующая теорема о трех полюсах: если R есть z-сфера, Q(z)dz² - квадратичный дифференциал на R, имеющий не более трех различных полюсов, то множество Ф̂ пусто.

Лит.: [1] Дженкинс Дж., Однолистные функции и конформные отображения, пер. с англ., М., 1962; [2] Jenkins J. A., «Illinois Math. J.», 1960, v. 4, № 3, p. 405-12.

Г. В. Кузьмина.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.