ГЛАДКОСТИ МОДУЛЬ

ГЛАДКОСТИ МОДУЛЬ - модуль непрерывности производной порядка m ≥ 1 функции f(x), определенной на банаховом пространстве X, т. е. выражение

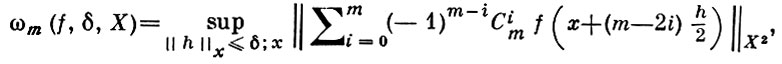
где (x ± mh/2) ⊂ X. При m = 1 Г. м.- обычный непрерывности модуль функции f(x). Основные свойства Г. м. (для случая X = ℂ - пространство непрерывных функций):

ω_m(f, 0, ℂ) = 0; ω_m(f, δ, ℂ) не убывает вместе с δ;

если k - целое ≥1, то

ω_m(f, kδ, ℂ) ≤ k^mω_m(f, δ, ℂ);

для любого λ > 0

ω_m(f, λδ, ℂ) ≤ (λ + 1)^mω_m(f, δ, ℂ);

если ν > m, то

ω_ν(f, δ, ℂ) ≤ 2^ν-mω_m(f, δ, ℂ);

если ν > m, то

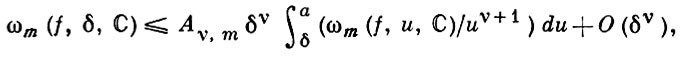
где A_ν,m и а - постоянные, не зависящие от f.

Нек-рые вопросы теории приближения функций могут получить окончательное решение только в терминах Г. м. порядка m ≥ 2. В теории приближения функций важен класс непрерывных периода 2π функций, Г. м. 2-го порядка к-рых удовлетворяет условию

ω₂(f, δ, С_2π) ≤ δ.

Модуль непрерывности таких функций удовлетворяет условию

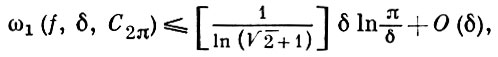
0 < δ ≤ π, причем постоянная 1/ln(√2 + 1) не может быть улучшена (см. [4]).

Лит.: [1] Бернштейн С. Н., Собр. сочинений, т. 1, с. 37, М., 1952; [2] Marchaud A., «J. math, pures et appl.», 1927, t. 6, p. 337-425; [3] Zуgmund A., «Duke Math. J.», 1945, v. 12, p. 47-76; [4] Ефимов А. В., «Изв. АН СССР. Сер. матем.», 1957, т. 21, № 2, с. 283-88.

А. В. Ефимов.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.