ГЛАДКАЯ СХЕМА

ГЛАДКАЯ СХЕМА - обобщение понятия неособого алгебраического многообразия. Схема X (локально) конечного типа над полем k наз. гладкой схемой (над k), если схема, полученная из X с помощью замены поля констант k на его алгебраич. замыкание k̅, является регулярной схемой, т. е. все ее локальные кольца регулярны. Для совершенного поля k понятия Г. с. над k и регулярной схемы над k совпадают. В частности, Г. с. конечного типа над алгебраически замкнутым полем есть неособое алгебраич. многообразие. В случае поля комплексных чисел неособое алгебраич. многообразие обладает структурой комплексного аналитического многообразия.

Схема является Г. с. тогда и только тогда, когда она может быть покрыта гладкими окрестностями. Точка схемы X наз. простой точкой схемы, если в нек-рой ее окрестности схема X есть Г. с; в противном случае точка наз. особой точкой схемы. Связная Г. с. неприводима. Произведение Г. с. снова есть Г. с; вообще, если Y есть Г. с. над k, а f : X → Y - гладкий морфизм, то X есть Г. с. над k.

Аффинное пространство Аⁿ_k и проективное пространство ℙⁿ_k являются Г. с. над k; над совершенным полем любая алгебраич. группа (т. е. приведенная алгебраич. схема групп) есть Г. с. Приведенная схема над алгебраич. замкнутым полем является Г. с. на всюду плотном открытом множестве.

Если схема X задается уравнениями

F_i(X₁, ..., X_m) = 0, i = 1, ...,n,

в аффинном пространстве А^m_k, то точка х ∈ Х будет простой тогда и только тогда, когда ранг матрицы Якоби

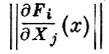
равен m - d, где d - размерность X в точке х (якобиевый критерий). В более общем случае, замкнутая подсхема X Г. с. Y, задаваемая пучком идеалов I, будет Г. с. в окрестности точки х в том и только в том случае, если существует система образующих g₁, ..., g_n идеала I_x в кольце О_X,x, удовлетворяющая тому условию, что dg₁, ..., dg_n составляют часть базиса свободного О_X,x-модуля пучка дифференциалов ΩО_X/k,x.

Лит.: [1] Шафаревич И. Р., Основы алгебраической геометрии, М., 1972; [2] Grothendieck A., «Publ. math. IHES», 1967, t. 32; [3] Zariski О., «Trans. Amer. Math. Soc.», 1947, v. 62, № 1, p. 1-52.

В. И. Данилов, И. В. Долгачев.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.