ГЛАВНЫХ ИДЕАЛОВ КОЛЬЦО

ГЛАВНЫХ ИДЕАЛОВ КОЛЬЦО - ассоциативное кольцо R с единицей, в к-ром все левые и правые идеалы являются главными, т. е. имеют вид Ra и аR, соответственно, где a ∈ R. Примеры Г. и. к.: кольцо целых чисел, кольцо многочленов F(х) над полем F, кольцо косых многочленов F(x, S) над полем F с автоморфизмом S : F → F (элементы F(x, S) имеют вид

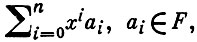
сложение этих элементов обычное, a умножение определяется законами дистрибутивности и равенством ax = xa^S, где а ∈ F), кольцо дифференциальных многочленов F(x, ') над полем F с дифференцированием ': F → F (это кольцо также состоит из элементов

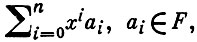
причем сложение обычное, а умножение определяется равенством ах = ха + а', где а ∈ F). Г. и. к. без делителей нуля наз. областью главных идеалов. Коммутативное Г. и. к. является прямой суммой областей главных идеалов и Г. и. к., обладающих единственным простым идеалом, к-рый нильпотентен (см. [2], с. 282). Если R - область главных идеалов, то два ненулевые элемента a, b кольца R имеют наибольший общий левый делитель (а, b) и наименьшее общее правое кратное [а, b], к-рые определяются как элементы, удовлетворяющие равенствам:

aR + bR = (a, b) R; aR ∩ bR = [а, b] R.

Элементы (a, b) и [a, b] единственны с точностью до обратимого правого множителя. Область главных идеалов является областью с однозначным разложением на множители. Двусторонние идеалы области главных идеалов образуют относительно умножения свободную коммутативную полугруппу с нулем и единицей (свободными порождающими этой полугруппы будут максимальные идеалы кольца).

Подмодуль N свободного модуля М конечного ранга n над R является свободным модулем ранга k ≤ n над R, и в модулях M и N можно так выбрать базисы a1, ..., аn и b1, ..., bk, что bi = eiai, 1 ≤ i ≤ k, где еi ∈ R и выявляется полным (т. е. eiR ∩ Rei ⊇ RejR) делителем элементов ej при i < j. Каждый конечно порожденный модуль К над R является прямой суммой циклич. модулей R/eiR, 1 ≤ i ≤ m, где еi ∈ R и еi - полный делитель ej при i < j, еi ≠ 0. Эта теорема обобщает основную теорему о конечно порожденных абелевых группах. Элементы еi, 1 ≤ i ≤ m, из предыдущей теоремы определены однозначно с точностью до подобия (см. Ассоциативные кольца и алгебры). Эти элементы наз. инвариантными множителями модуля K. Кроме того, модуль K можно представить в виде прямой суммы далее неразложимых циклич. модулей R/qiR, где qi ∈ R, 1 ≤ i ≤ k;. Элементы qi, 1 ≤ i ≤ k, определены однозначно с точностью до подобия и наз. элементарными делителями модуля К. Если область R главных идеалов коммутативна, то qiR = 0 или qiR = pniiR, 1 ≤ i ≤ k, где рi - неприводимые (простые) элементы кольца R. Из предыдущих утверждений вытекают обычные свойства элементарных делителей и инвариантных множителей линейных преобразований конечномерных векторных пространств [3].

Лит.: [1] Джекобсон Н., Теория колец, пер. с англ., М., 1947; [2] Зарисский О., Самюэль П., Коммутативная алгебра, пер. с англ., т. 1, М., 1963; [3] Бурбаки Н., Алгебра. Модули, кольца, формы, пер. с франц., М., 1966.

Л. А. Бокуть.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.