ГЛАВНЫЙ ФАКТОР

ГЛАВНЫЙ ФАКТОР полугруппы - всякая факторполугруппа Риса (см. Полугруппа) вида J(х)/N(х), где J(х) - двусторонний главный идеал данной полугруппы, порожденный элементом х, a N(x) = J(x)\J_x, где J_x есть 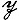-класс (см. Грина отношения эквивалентности), содержащий х; если множество N(х) не пусто, то оно является идеалом, а в случае, когда N(x) = ∅, считается J(х)/N(х) = J(х). Г. ф. полугруппы наз. также идеальным фактором. Произвольный Г. ф. полугруппы есть либо полугруппа с нулевым умножением, либо 0-простая полугруппа, либо идеально простая полугруппа (см. Простая полугруппа); последнее имеет место тогда и только тогда, когда полугруппа обладает ядром и данный Г. ф. совпадает с ядром. Полугруппа, не имеющая Г. ф. с нулевым умножением, наз. полупростой; полупростота полугруппы эквивалентна, напр., тому, что для любого ее двустороннего идеала А выполняется равенство А² = А. Всякая регулярная полугруппа полупроста. Если каждый Г. ф. полугруппы либо вполне 0-прост, либо вполне прост (см. Вполне простая полугруппа), то полугруппа наз. вполне полупростой. Полугруппа вполне полупроста тогда и только тогда, когда она регулярна и удовлетворяет любому из следующих двойственных друг другу условий: для каждого 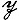-класса частично упорядоченное множество содержащихся в нем ℒ-классов (соответственно ℛ-классов) обладает минимальным элементом; при этом = .

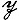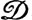Произвольная полугруппа как бы собрана из своих Г. ф., это объясняет, в частности, особую роль, к-рую играют в теории полугрупп идеально простые и 0-простые полугруппы.

Лит.: [1] Ляпин Е. С., Полугруппы, М., 1960; [2] Клиффорд А., Престон Г., Алгебраическая теория полугрупп, пер. с англ., тт. 1-2, М., 1972.

Л. Н. Шеврин.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.