ГЛАВНЫЙ G-ОБЪЕКТ

ГЛАВНЫЙ G-ОБЪЕКТ в топологизированной категории - понятие теории категорий, частные случаи которого - главное расслоение в топологии, главное однородное пространство в алгебраич. геометрии и др. Пусть G - групповой объект категории С с произведениями и финальным объектом е. Объект Р наз. G-объектом, если определен морфизм π: P × G → P, для к-рого коммутативны следующие диаграммы:

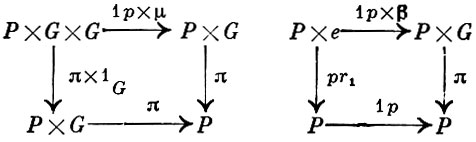
Здесь μ : G × G → G - морфизм группового закона на G, а β : е → G - морфизм единичного элемента G. Более точно, введенные выше G-объекты наз. правыми G-объектами, аналогично дается определение левых G-oбъектов. Примером G-объекта может служить сам групповой объект G, для к-рого отображение μ совпадает с отображением π. Такой объект наз. тривиальным G-oбъектом. G-объекты категории С образуют подкатегорию С^G, морфизмами в к-рой служат морфизмы, перестановочные с морфизмами π. G-объект наз. формально главным G-oбъектом, если морфизмы Р × G -→^pr₁ Р и Р × G -→^π Р индуцируют изоморфизм φ = πрr₁ : P × G #&8594; P × P. Если Т - некоторая топология Гротендика на категории С, то формально главный G-объект Р наз. главным G-объектом (относительно топологии Т), если существует покрытие (U_i → e)i ∈ I финального объекта такое, что для любого i ∈ I произведение G ×_e U_i изоморфно тривиальному G ×_e U_i-объекту.

Примеры. 1) Если С - категория множеств, а G - группа, то непустые G-объекты наз. G-множествами. Это множества Р, для к-рых задано такое отображение P × G → P ((р, g) → pg), что для любых g, g' ∈ G имеет место р(gg') = (pg)g' и для любого р ∈ Р верно р ⋅ 1 = р. Главный G-объект есть G-множество, в к-ром для любых р, р' ∈ Р существует единственный элемент g ∈ G такой, что pg = p' (главное однородное G-множество). Если Р не пусто, то выбор р₀ ∈ Р определяет отображение g → p₀g, к-рое устанавливает изоморфизм Р и тривиального G-множества G. Тем самым в любой топологии формально главный G-объект является главным G-объектом.

2) Если X - дифференциируемое многообразие, Н - группа Ли, то, взяв за С категорию расслоений над X, за групповой объект G проекцию Н × Х → Х и определив топологию в С с помощью семейств открытых покрытий, можно получить определение главного G-расслоения.

Если Р - формально главный G-объект категории С, то для любого объекта X категории Ob(С) множество Р(X) = Hom_C(X, Р) либо пусто, либо является главным однородным G(X)-множеством.

G-объект Р изоморфен тривиальному G-объекту тогда и только тогда, когда существует сечение е → Р. Множество классов G-объектов (относительно отношения изоморфизма между ними) обозначается через H¹(С, G). В случае, когда G - абелев групповой объект, множество H¹(С, G) с отмеченной точкой, соответствующей классу тривиальных G-объектов, является группой и вычисляется стандартными средствами гомологич. алгебры. В общем случае вычисления H¹(С, G) используют конструкции когомологий Чеха (см. Неабелевы когомологий).

Лит.: [1] Revêtements etales et groupe fondamental, В., 1971.

И. В. Долгачев.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.