ГЛАВНОЕ ФУНДАМЕНТАЛЬНОЕ РЕШЕНИЕ

ГЛАВНОЕ ФУНДАМЕНТАЛЬНОЕ РЕШЕНИЕ - фундаментальное решение G(x, у) определенного во всем пространстве Еⁿ эллиптич. уравнения 2-го порядка

(*)

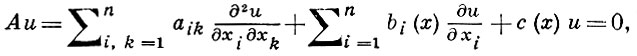
удовлетворяющее условиям

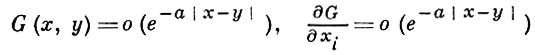
для нек-рых положительных постоянных а и R при |x - y| > R.

Если коэффициенты а_ik(x), b_i(х) и с(х) удовлетворяют в Еⁿ условию Гёльдера и для γ > 0 выполняется неравенство c(x) < -γ, то Г. ф. р. существует. В случае, когда коэффициенты оператора А определены в нек-рой ограниченной области с достаточно гладкой границей, их можно продолжить на все пространство Еⁿ так, что у продолженного оператора Г. ф. р. будет существовать.

Лит.: [1] Миранда К., Уравнения с частными производными эллиптического типа, пер. с итал., М., 1957.

Ш. А. Алимов.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.