
ГЛАВНОЕ РАССЛОЕНИЕ
ГЛАВНОЕ РАССЛОЕНИЕ - G-расслоение πG: Х → В такое, что группа G действует свободно и совершенно на пространстве X. Значение Г. р. состоит в том, что оно позволяет строить ассоциированные (с ним) расслоения со слоем F, если задано представление G в группе гомеоморфизмов F. Дифференцируемые Г. р. с группами Ли играют важную роль в теории связностей и групп голономии. Пусть, напр., Н - топологич. группа, имеющая G своей замкнутой подгруппой, H/G - однородное пространство левых смежных классов Н по G, тогда расслоение πG: H → H/G является Г. р. Пусть, далее, ХG - конструкция Милнора, т. е. соединение бесконечного числа экземпляров группы G, каждая точка к-рого имеет вид:
〈g, 0〉 = 〈g0t0, g1t1, ...〉,
где gi ∈ G, ti ∈ [0, 1], причем только конечное число ti отлично от нуля и Σti = 1. Действие группы G на XG, определенное формулой h〈g, t〉 = 〈hg, t〉, свободно, и расслоение ωG : XG → XG mod G является нумерируемым Г. p.
Каждый слой Г. р. гомеоморфен группе G.
Морфизм Г. р. - это морфизм расслоений f : πG → πG', для к-рого отображение слоев fπ-1G(b) индуцирует гомоморфизм групп
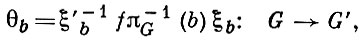
где ξb(g) = gх, πG(x) = b. В частности, морфизм наз. эквивариантным, если θb = θ не зависит от b, так что gf(x) = θ(g)f(x) для любых х ∈ Х, g ∈ G; если G = G' и θ = id, то эквивариантный морфизм наз. G-морфнзмом. Любой G, B-морфизм (т. е. G-морфнзм Г. р. над В) является G-изоморфизмом.
Для любого отображения u: В'→ В и Г. р. πG: X → B индуцированное расслоение u*(πG) является Г. р. с той же группой G, причем отображение U : u*(πG) → πG является G-морфизмом, однозначно определяющим действие G на пространстве u*(х). Напр., если Г. р. πG тривиально, то оно изоморфно Г. р. φ*(η), где η есть G-расстояние над одной точкой, φ - постоянное отображение. Обратное также верно, и потому Г. р., обладающее сечением, тривиально. Для каждого нумерируемого Г. р. πG : X → В существует такое отображение f : B → XG mod G, что f*(ωG) является G-изоморфным πG; при этом для изоморфности Г. р. f*0(ωG) и f*1(ωG) необходима и достаточна гомотопность f0 и f1. Это - основная теорема гомотопической классификации Г. р., выражающая универсальность Г. p. ωG (полученного с помощью конструкции Милнора) по отношению к классифицирующему отображению f.
Лит.: [1] Бишоп Р. Л., Криттенден Р. Дж., Геометрия многообразий, пер. с англ., М., 1967; [2] Номидзу К., Группы Ли и дифференциальная геометрия, пер. с англ., М., 1960; [3] Стернберг С., Лекции по дифференциальной геометрии, пер. с англ., М., 1970; [4] Расслоенные пространства и их приложения, сб. переводов, М., 1958; [5] Стинрод Н., Топология косых произведений, пер. с англ., М., 1953; [6] Хьюзмоллер Д., Расслоенные пространства, пер. с англ., М., 1970.
А. Ф. Щекутьев.
Источники:
- Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'