ГЛАВНОЕ ОДНОРОДНОЕ ПРОСТРАНСТВО

ГЛАВНОЕ ОДНОРОДНОЕ ПРОСТРАНСТВО - главный G-объект в категории алгебраич. многообразий или схем. Если S - схема, а Г - схема групп над S, то главный G-объект в категории схем над Г наз. Г. о. п. над S. В случае, когда S - спектр поля k и Г - алгебраическая k-группа, Г. о. п. над Г есть алгебраическое k-многообразие V, на к-ром Г действует (слева), и при замене k на его сепарабельное алгебраич. замыкание k, каждая точка v ∈ V(k̅) определяет изоморфное отображение g → gv многообразий V_k̅ и F_k̅. Г. о. п. V тривиально тогда и только тогда, когда V(k) не пусто. Множество классов, изоморфных Г. о. п., над гладкой алгебраич. группой Г может быть отождествлено с множеством Галуа когомологий Н¹(k, Г). В общем случае множество классов Г. о. п. над S-схемой групп Г совпадает с множеством одномерных неабелевых когомологий H¹(S_T, Г), где S_T - некоторая топология Гротендика на схеме S [2].

В ряде случаев Г. о. п. вычислено. Если k -конечное поле, то каждое Г. о. п. над связной алгебраической k-группой является тривиальным (теорема Ленга). Это же утверждение верно, если k - поле р-адических чисел, а Г - односвязная и полупростая группа (теорема Кнезера). Если Г = Г_m,S - мультипликативная S-схема групп, то множество классов Г. о. п. над Г совпадает с Пикара группой Pic(S) схемы S. В частности, если S - спектр поля, то эта группа тривиальна. Если Г = Г_a,S - аддитивная S-схема групп, то множество классов Г. о. п. над Г совпадает с группой H¹(S, 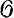) одномерных когомологий структурного пучка 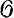_S схемы S. В частности, это множество тривиально, если S - аффинная схема. В случае, когда k - глобальное поле (т. е. поле алгебраич. чисел или поле алгебраич. функций от одного переменного), изучение множества классов Г. о. п. над алгебраической k-группой Г основано на исследовании множества Тейта-Шафаревича III(Г), состоящего из Г. о. п. над Г, имеющих рациональные точки во всех пополнениях k_V относительно нормирований поля k. В случае, когда Г - абелева группа над полем k, множество классов Г. о. п. над Г образует группу (см. Вейля-Шатле группа).

Лит.: [1] Серр Ж.-П., Когомологий Галуа, пер. с франц., М., 1968; [2] Demazure М., Gabriel P., Groupes algebriques, t. 1, P.-Amst., 1970; [3] Lang S., Tate J., «Amer. J. Math.», 1958, v. 80, p. 659-84.

В. E. Воскресенский, И. В. Долгачев.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.