ГЛАВНОЕ АНАЛИТИЧЕСКОЕ РАССЛОЕНИЕ

ГЛАВНОЕ АНАЛИТИЧЕСКОЕ РАССЛОЕНИЕ - локально тривиальное аналитич. расслоение, на слоях к-рого просто транзитивно и аналитически действует структурная группа Ли; то есть Г. а. р. есть четверка (Р, В, G, π), где Р, В - аналитические пространства над полем k, π : Р → В аналитич. отображение, G - группа Ли над k, аналитически действующая справа на Р, причем для каждого элемента базы В существуют окрестность U и аналитич. изоморфизм

φ : U × G → π^-1(U)

такой, что

φ(х, gh) = φ(х, g)h, x ∈ U, g, h ∈ G.

Каждое векторное аналитическое расслоение р: V → B с n-мерным слоем определяет Г. а. р. с базой В и группой GL(n, к), слоем к-рого над точкой b ∈ В является многообразие всех базисов слоя р^-1(b). Это частный случай взаимно однозначного соответствия между аналитич. расслоениями с заданным слоем и структурной группой G и ассоциированными с ними Г. а. р. Другие примеры Г. а. р.: расслоение H → H/G, слоями к-рого служат левые смежные классы группы Ли Н по ее подгруппе Ли G; аналитич. накрытие (здесь структурная группа - группа накрытия).

Г. а. р. можно задать при помощи открытого покрытия {U_i}_i∈I его базы B и функций перехода, т. е. аналитич. отображений

g_ij: U_i ∩ U_j → G, i, j ∈ I, U_i ∩ U_j ≠ ∅,

удовлетворяющих условиям

g_ij(x)g_jk(x) = g_ik (*), x ∈ U_i ∩ U_j ∩ U_k.

Функции перехода образуют одномерный коцикл со значениями в пучке 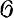^G ростков аналитич. отображений B → G, что дает взаимно однозначное соответствие между множеством Г. а. р. с базой В и группой G и множеством когомологий H¹(В, 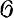^G). Классификация Г. а. р. с базой В и структурной группой G представляет собой (для неабелевой группы G) проблему, решенную лишь в нек-рых специальных случаях (по поводу соответствующей проблемы локальных модулей см. Деформация аналитической структуры). Связь между этой классификацией и классификацией топологических главных расслоений выражается естественным отображением

α: H¹(В, 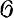^G) → H¹(В, C^G),

где С^G - пучок ростков непрерывных отображений B → G.

Пусть k = ℂ, а В - приведенное Штейна пространство, тогда отображение α биективно, и проблема классификации сводится к задаче гомотопич. топологии [4]. В частности, всякое Г. а. р., базой к-рого является некомпактная риманова поверхность, а структурная группа связна, тривиально. Результат работы [4] получен на самом деле для более широкого класса E-главных расслоений, в определении к-рых группа G заменяется некоторым аналитическим локально тривиальным расслоением Е → В на комплексные группы Ли, послойно действующим на Р. Существует обобщение приведенного результата на случай, когда структурная группа есть банахова комплексная группа Ли [2]. Если же В - компактная риманова поверхность, то α cюръективно, но не инъективно. В общем случае α не обязано быть ни инъективным, ни сюръективным. Для связной разрешимой группы G известны когомологич. достаточные условия инъективности или биективности отображения α [3].

Изучен также случай, когда В - компактная риманова поверхность рода р, a G - связная редуктивная алгебраич. группа. Для р = 0 соответствующая классификация дана в [5], для р = 1 при G = GL(n, ℂ) - в [1]. В случае р ≥ 2, G = GL(n, ℂ) (см. Векторное алгебраическое расслоение) существенную роль играет понятие стабильного векторного расслоения. Это понятие обобщается [6] на случай произвольной связной редуктивной группы G. Множество всех стабильных главных расслоений данного топологич. типа на компактной римановой поверхности обладает естественной структурой связного нормального комплексного пространства. Получена также частичная классификация векторных расслоений над комплексным проективным пространством В = Р^m(ℂ) и над алгебраическими поверхностями.

О вещественных Г. а. р. (случай k = ℝ) см. Вещественное аналитическое пространство.

Лит.: [1] Atiуah М., «Рrос. London Math. Soc.», 1957, v. 11, № 27, p. 417-52; [2] Вungart L., «Topology», 1968, v. 7, № 1, p. 55-68; [3] Frenkel J., «Bull. Soc. Math. France», 1957, t. 85, № 2, p. 135-220; [4] Grauert H., «Math. Ann.», 1958, Bd 135, № 3, S. 263-73; [5] Grothendieck A., «Amer. J. Math.», 1957, v. 79, № 1, p. 121-38; [6] Ramanathan A., «Math. Ann.», 1975, Bd 213, № 2, S. 129-52.

А. Л. Онищик.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.