ГИПОЦИКЛОИДА

ГИПОЦИКЛОИДА - плоская кривая, траектория точки окружности, катящейся по другой окружности и имеющей с ней внутреннее касание. Параметрич. уравнения:

x = (R - r) cos θ + r cos [(R - r)θ/r],

y = (R - r) sin θ - r sin [(R - r)θ/r],

где r - радиус катящейся окружности, R - радиус неподвижной окружности, θ - угол, стягиваемый дугой между точками касания окружностей. В зависимости от величины модуля m = R/r получаются Г. различной формы. При m целом кривая состоит из m непересекающихся ветвей (см. рис. а). Точки возврата A₁, ..., A_m имеют полярные координаты ρ = R, φ = 2kπ/m, k = 0, 1, ..., m-1. При m иррациональном число ветвей бесконечно, точка М в исходное положение не возвращается; при m рациональном Г. (см. рис., б) -замкнутая алгебраич. кривая. Длина дуги от точки θ = 0:

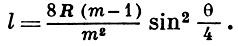
Радиус кривизны:

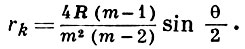
Если точка находится не на катящейся окружности, а лежит вне (внутри) ее, то кривая наз. удлиненной (укороченной) гипоциклоидой или гипотрохоидой (см. Трохоида). При m = 2

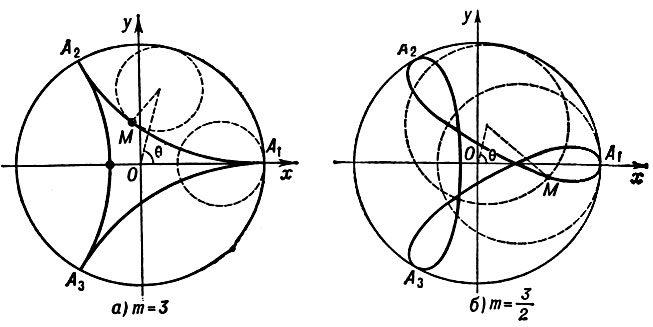
Г.- отрезок прямой, при m = 3 - Штейнера кривая, при m = 4 - астроида. Г. относится к так наз. циклоидальным кривым.

Лит.: [1] Савелов А. А., Плоские кривые, М., 1960.

Д. Д. Соколов.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.