ГИПЕРЭЛЛИПТИЧЕСКИЙ ИНТЕГРАЛ

ГИПЕРЭЛЛИПТИЧЕСКИЙ ИНТЕГРАЛ - частный случай абелева интеграла

∫ R(z, w)dz, (1)

где R - рациональная функция от переменных z, w, связанных алгебраич. уравнением частного вида

w² = P(z), (2)

здесь P(z) - многочлен степени m ≥ 5 без кратных корней; при m = 3, 4 получаются эллиптические интегралы, случай m = 5, 6 иногда наз. ультраэллиптическим.

Уравнению (2) соответствует двулистная компактная риманова поверхность F рода g = (m - 2)/2, если m -четно, и рода g = (m - 1)/2, если m - нечетно; таким образом, в случае Г. и. g ≥ 2. На F функции z, w, а следовательно и R(z, w), однозначны. Интеграл (1), рассматриваемый как определенный, задается на F как криволинейный интеграл от аналитич. функции, взятый вдоль нек-рого спрямляемого пути L, причем, вообще говоря, задание только начальной и конечной точек пути L не вполне определяет значение интеграла (1).

Как и в общем случае абелевых интегралов, любой Г. и. можно выразить в виде линейной комбинации элементарных функций и канонических Г. и. I, II, III родов, имеющих свой специфич. вид. Так, нормальные Г. и. I рода являются линейными комбинациями Г. и. I рода вида

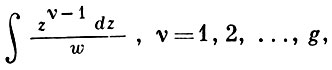
где (z^ν-1/w)dz, ν = 1, 2, ..., g, - простейший базис абелевых дифференциалов I рода для случая гиперэллиптич. поверхности F. Явные выражения для абелевых дифференциалов II и III родов и для соответствующих Г. и. также легко выписываются (см. [2]). В основных чертах теория Г. и. совпадает с общей теорией абелевых интегралов.

Все рациональные функции R(z, w) от z и w образуют гиперэллиптическое поле алгебраич. функций, соответствующее данному уравнению (2) и имеющее род g. Всякая компактная риманова поверхность рода g = 1 или g = 2 допускает эллиптическое или гиперэллиптич. поле, соответственно. Однако уже при g = 3 существуют компактные римановы поверхности F более сложной структуры, не обладающие этим свойством.

Лит.: [1] Спрингер Дж., Введение в теорию римановых поверхностей, пер. с англ., М., 1960, гл. 10; [2] Неванлинна Р., Униформизация, пер. с нем., М., 1955, гл. 5; [3] Neumann К., Vorlesungen über Riemanns Theorie der Abelschen Integrate, Lpz., 1884.

E. Д. Соломенцев.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.