ГИПЕРПРОСТРАНСТВО

ГИПЕРПРОСТРАНСТВО над топологическим пространством X - пространство, точками к-рого являются элементы нек-рого семейства 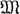подмножеств пространства X с той или иной топологией. Обычно 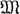- кольцо множеств, хотя априори это не предполагается.

Пример. Р(X) - Г. всех подмножеств пространства X; базу топологии образуют множества {М, F ⊂ M ⊂ G} при условии, что F замкнуто в X, G открыто в X и F ⊂ G.

Наиболее распространенным является Г. 2^X, состоящее из всех замкнутых подмножеств топологич. пространства X; предбазу экспоненциальной топологии на 2^X образуют множества {F, F ⊂ G} и {F, F ∩ H ≠ ∅}, где G и Н открыты в X, а F пробегает 2^X. Аналогично определяется топология в следующих Г.: во множестве (Х) всех бикомпактных подмножеств пространства X, во множестве Ехр_ω(X) всех конечных подмножеств пространства X, во множестве K(X) всех подконтинуумов (связных бикомпактов) континуума X и т. и. Эти пространства могут рассматриваться как подпространства Г. 2^X, взятого с экспоненциальной топологией. Если X - равномерное пространство, то множество 2^X наделяется естественной равномерной структурой; получающееся при этом равномерное пространство обозначается через H(X). Если X - бикомпакт, то Г. 2^X, (X) и Н(X) гомеоморфны между собой и являются бикомпактами. Если X - компактное метризуемое пространство, то таково же и 2^X. Если X - континуум, то 2^X и K(X) - тоже континуумы.

Лит.: [1] Куратовский К., Топология, пер. с англ., т. 1-2, М., 1966-69; [2] Michael Е., «Trans. Amer. Math. Soc.», 1951, v. 71, № 1, p. 152-82; [3] Пономарев В. И., «Матем. сб.», 1959, т. 48(90), № 2, с. 191-212.

Б. А. Ефимов.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.