ГИПЕРПОВЕРХНОСТЬ

ГИПЕРПОВЕРХНОСТЬ - 1) Обобщение понятия обычной поверхности трехмерного пространства на случай n-мерного пространства. Размерность Г. на единицу меньше размерности объемлющего пространства.

2) Если М и N - дифференцируемые многообразия, dim N - dim М = 1 и определено погружение f : M → N, то f(M) - Г. в N. Здесь f - дифференцируемое отображение, дифференциал к-рого df в любой точке х ∈ М является инъективным отображением пространства М_x, касательного к M в точке х, в пространство N_f(x), касательное к N в точке f(x).

В. Т. Базылев.

3) Г. алгебраическая - подмногообразие алгебраич. многообразия, локально задаваемое одним уравнением. Г. а. в аффинном пространстве Аⁿ_k над полем k задается глобально одним уравнением

f(x₁, ..., x_n) = 0.

Г. а. W в проективном пространстве Pⁿ_k задается уравнением

F(x₀, ..., x_n) = 0,

где F - однородная форма от n + 1 переменных. Степень m этой формы наз. степенью (порядком) гиперповерхности. Замкнутая подсхема W схемы V наз. гиперповерхностью, если соответствующий пучок идеалов I_W ⊂ O_V является пучком главных идеалов. Для связных неособых алгебраич. многообразий это условие означает, что коразмерность W в V равна единице. Для каждой неособой Г. а. W ⊂ Pⁿ_k порядка m (обозначаемой часто через V^m_n) имеют место следующие факты:

канонич. класс K_W равен (m - n - 1)H_W, где H_W - класс гиперплоского сечения W;

группы когомологий Hⁱ(W, О_W) = 0 для i ≠ 0, n - 1, а

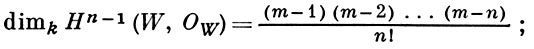
при n ≥ 3 фундаментальная группа (алгебраическая или топологическая, если k = ℂ) π₁(W) = 0;

при n ≥ 4 группа Пикара Pic(W) ≃ Z и порождается классом гипергеометрического сечения.

И. В. Долгачев.

4) Г. аналитическая (Г. а.) - множество S в комплексном евклидовом пространстве ℂⁿ, к-рое в окрестности каждой своей точки ζ ∈ S задается уравнением f_ζ(z, t) = 0, где функция f_ζ(z, t) непрерывна по параметру t ∈ (-ε, ε), ε > 0, и при каждом фиксированном t голоморфна по z в независящей от t окрестности U_ζ ∋ ζ, причем Σ|∂f/∂z_j| ≠ 0 для всех (z, t) ∈ U_ζ × (-ε, ε).

Другими словами, Г. а. есть множество в ℂⁿ, к-рое локально является объединением непрерывного однопараметрич. семейства комплексноаналитич. поверхностей комплексной коразмерности 1. Напр., если функция f голоморфна в области D ⊂ ℂⁿ и grad f ≠ 0 в D, то множества |f| = 1, Rе f = 0 и т. п. являются Г. а.

Дважды гладкая гиперповерхность S в ℝ²ⁿ = ℂⁿ является Г. а. тогда и только тогда, когда ее форма Леви тождественно на S равна нулю или когда S локально псевдовыпукла с обеих сторон.

Е. М. Чирка.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.