ГИПЕРКОМПЛЕКСНОЕ ЧИСЛО

ГИПЕРКОМПЛЕКСНОЕ ЧИСЛО - элемент конечномерной алгебры с единицей над полем действительных чисел R (ранее называвшейся гиперкомплексной системой). Исторически Г. ч. возникли как обобщение комплексных чисел. Действия над комплексными числами соответствуют простейшим геометрич. преобразованиям плоскости (сдвигу, вращению, растяжению и их комбинациям). При попытках построить числа, к-рые играли бы для трехмерного пространства роль комплексных чисел для плоскости, выяснилось, что здесь не может быть полной аналогии; это привело к созданию и развитию теории систем Г. ч.

Гиперкомплексная система ранга n получается введением умножения в n-мерном действительном пространстве ℝⁿ, удовлетворяющего аксиомам алгебры над полем. Пусть 1 - единица гиперкомплексной системы и 1, i₁, i₂, ..., i_n-1 - некоторый базис пространства ℝⁿ. Г. ч.

α̅ = а₀ - a₁i₁ - ... - а_ni_n

из гиперкомплексной системы U наз. сопряженным Г. ч.

α̅ = а₀ + a₁i₁ + ... + а_ni_n

Пусть U⁽²⁾ = {u₁ + u₂e}, где u₁, u₁₂ ∈ U, а е - некоторый новый символ. Множество U⁽²⁾ можно превратить в гиперкомплексную систему, определяя сложение формулой

(u₁ + u₂e) + (v₁ + v₂e) = (u₁ + v₁) + (u₂ + v₂)e

и умножение формулой

(u₁ + u₂e)(v₁ + v₂e) = (u₁v₁ - v̅₂u₂) + (v₂u₁ + u₂v̅₁)е.

Гиперкомплексная система U⁽²⁾ наз. удвоением гиперкомплексной системы U.

Примеры гиперкомплексных систем: действительные числа, комплексные числа, кватернионы, Кэли числа (в этом перечне каждая следующая система получается из предыдущей удвоением). Другие примеры - системы двойных и дуальных чисел, Г. ч. вида

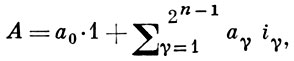
при n = 4, наз. числами Клиффорда-Липшица (эти Г. ч. являются элементами Клиффорда алгебр ранга 2ⁿ). Важным примером гиперкомплексных систем являются полные матричные алгебры над ℝ.

Иногда в определение системы Г. ч. включают требование ассоциативности умножения или отождествляют понятие алгебры и гиперкомплексной системы.

Лит.: [1] Кантор И. Л., Солодовников А. С., Гиперкомплексные числа, М., 1973; [2] Калужнин Л. А., Введение в общую алгебру, М., 1973.

Н. Н. Вильямc.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.