ГИПЕРКОМПЛЕКСНОГО ПЕРЕМЕННОГО ФУНКЦИЯ

ГИПЕРКОМПЛЕКСНОГО ПЕРЕМЕННОГО ФУНКЦИЯ - функция w(z) гиперкомплексного переменного z (см. Гиперкомплексное число) над полем действительных чисел, т. е. функция на конечномерной ассоциативной алгебре 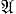. В более узком смысле под Г. п. ф. понимается функция w(z) со значениями в той же алгебре 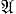, т. е. функция w(z) может быть представлена в виде

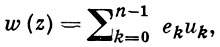
где e_k, k = 0, 1, ..., n-1,- базис алгебры 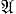, а u_k = u_k(х₀, x₁, ..., х_n-1), k = 0, 1, ..., n - 1, - система n действительных функций от n действительных переменных. Теория Г. п. ф. наиболее развита в случае, когда 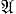есть алгебра кватернионов.

Аналитические (регулярные) Г. п. ф. представляют собой обобщения в различных направлениях аналитич. функций одного комплексного переменного. При этом, в силу неэквивалентности различных определений аналитичности в случае произвольной алгебры, существуют различные понятия аналитической Г. п. ф.

В современных исследованиях наибольшее внимание привлекают регулярные Г. п. ф. в смысле Фютера, или F-аналитические Г. п. ф. (см. [1]). Г. п. ф. w(z) наз. праворегулярной Г. п. ф. в точке z₀, если в этой точке справедливо дифференциальное уравнение (условие Фютера)

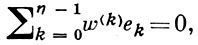
где

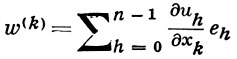
- частная производная функции w по x_k, причем все производные предполагаются непрерывными. Функция w(z) наз. леворегулярной Г. п. ф., если

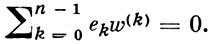
В случае некоммутативной алгебры 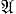эти понятия не равносильны. Сумма и разность праворегулярных Г. п. ф. праворегулярны, но для произведения и частного это неверно. Степени переменного z не праворегулярны. Имеются ряды Тейлора и Лорана по специально построенным аналогам степеней. Условие Фютера равносильно обращению в нуль дифференциала δω = 0 гиперкомплексной дифференциальной формы ω = wdz (для леворегулярных Г. п. ф.- формы ω = dzw); отсюда получается специфическая интегральная теорема.

Аналитической по Шефферсу Г. п. ф. [2] в точке z₀ для случая коммутативной алгебры 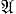наз. Г. п. ф., у к-рой дифференциал в этой точке может быть записан в виде

dw = φ(z)dz,

где производная φ(z) = dw/dz не зависит от dz. Это условие для коммутативной алгебры 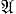равносильно тому, что dω = 0, и интеграл ∫wdz не зависит от пути; Г. п. ф., аналитические по Шефферсу, F-регулярны тогда и только тогда, когда

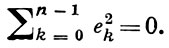
Г. п. ф. w(z) наз. аналитической по Хаусдорфу [3] в точке z₀, если ее дифференциал dw есть линейная функция от dz, то есть

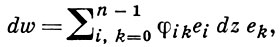
где φ_ik - действительные функции от х₀, х₁, ..., x_n-1. Аналог степенных рядов здесь строится проще, но интеграл зависит от пути. Для коммутативной алгебры 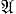определения Хаусдорфа и Шефферса эквивалентны.

Лит.: [1] Fueter К. R., «Elem. Math.», 1948, Bd 3, S. 89-94; [21 Sсhеffеrs G., «Bеr. Verhandl. Sächsisch. Akad. Wiss. Leipzig Math.-phys. Kl.», 1893, Bd 45, S. 828-48; [3] Hausdоrff F., там же, 1900, Bd 52, S. 43-61; [4] Кристалинский Р. X., «Уч. зап. Смоленского пед. ин-та», 1965, вып. 14, с. 91-95.

Е. Д. Соломенцев.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.