ГИПЕРГОМОЛОГИЙ ФУНКТОР

ГИПЕРГОМОЛОГИЙ ФУНКТОР - набор функторов 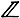_nF на категории комплексов, связанный с нек-рым функтором F. Именно, пусть F : А → В - ковариантный аддитивный функтор из абелевой категории А с достаточным числом проективных объектов в абелеву категорию В. Пусть далее K. - цепной комплекс со значениями в А и L.. - резольвента Картана-Эйленберга комплекса K., состоящая из проективных объектов. Тогда бикомплекс F(L..) определяет гомологии H_n(F(L..)) = 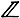_nF(K.) и две сходящиеся к ним спектральные последовательности с начальными членами

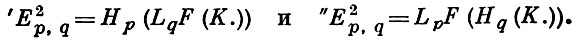
Эти гомологии и спектральные последовательности функториально зависят от K. и наз. соответственно функторами гипергомологий для F и спектральными функторами гипергомологий для F. Г. ф. 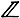. F является гомологич. функтором на категории комплексов в следующих важных случаях: когда F перестановочен с индуктивными пределами; когда объекты категории A имеют проективные резольвенты длины ≤n; если рассматривать его на категории комплексов с положительными степенями.

Двойственным образом определяются функторы гиперкогомологий.

Лит.: [1] Картан А., Эйленберг С., Гомологическая алгебра, пер. с англ., М., 1960; [2] Гротендик А., О некоторых вопросах гомологической алгебры, пер. с франц., М., 1961.

В. И. Данилов.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.