
ГИПЕРГЕОМЕТРИЧЕСКОЕ УРАВНЕНИЕ
ГИПЕРГЕОМЕТРИЧЕСКОЕ УРАВНЕНИЕ, уравнение Гаусса,- линейное обыкновенное дифференциальное уравнение 2-го порядка
z(z - 1)w'' + [(α + β + 1)z - γ]w' + αβw = 0, (1)
α, β, γ = const,
или, в самосопряженной форме,
[zγ(z - 1)α+β+1-γw']' + αβzγ-1(z - 1)α+β-γw = 0.
Переменные z, w и параметры α, β, γ в общем случае могут принимать любые комплексные значения. После подстановки
w = z-γ/2(z - 1)(γ-α-β-1)/2u
получается приведенная форма уравнения (1):
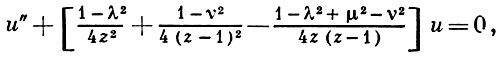
(2)
где λ = 1 - γ, μ = α - β, ν = γ - α - β.
Уравнение (1) подробно изучал К. Гаусс [1] в связи с развитой им теорией гипергеометрических рядов, но еще раньше это уравнение (и его решение) рассматривал Л. Эйлер (L. Euler).
Решения уравнения (1) выражаются через гипергеометрическую функцию F(α, β, γ; z). Если γ не равно целому числу, то общее решение уравнения (1) можно записать в виде
w = C1F (α, β, γ; х) + C2z1-γF(α - γ + 1, β - γ + 1, 2 - γ; z), (3)
где C1, С2 - произвольные постоянные; представление (3) справедливо в комплексной плоскости z с разрезами (-∞, 0) и (1, ∞). В частности, в действительном случае формула (3) дает общее решение уравнения (1) на интервале 0 < z < 1. Для целых значений γ общее решение имеет более сложный вид (возможно существование членов, содержащих логарифмы).
В качестве фундаментальной системы решений уравнения (1) можно выбирать и иные функции, отличные от указанных в (3). Напр., если α - β не равно целому числу, то
w = C1(-z)--αF(α, α - γ + 1, α - β + 1; z-1) + C2(-z)2(β - γ + 1, β, β - α + 1; z-1)
есть общее решение уравнения (1) в комплексной плоскости z с разрезом (0, ∞) (см. [2], [3]).
Г. у. включает как частные случаи ряд дифференциальных уравнений, встречающихся в приложениях; многие линейные обыкновенные дифференциальные уравнения 2-го порядка преобразованием неизвестной функции и независимой переменной приводятся к уравнению (1) (см. [4]). Особенно большое значение имеет близкое уравнению (1) вырожденное гипергеометрическое уравнение. Отношение s(z) двух линейно независимых решений уравнения (2) удовлетворяет Шварца уравнению, тесно связанному с задачей конформного отображения полуплоскости на треугольник, ограниченный тремя дугами окружностей. Изучение обратной функции z(s) приводит к понятию автоморфной функции (см. [5]).
Имеются линейные уравнения высших порядков, свойства решений к-рых аналогичны свойствам гипергеометрич. функции: решение уравнения (q+1)-го порядка
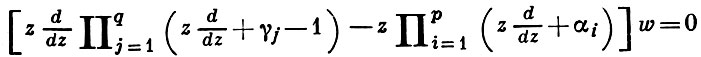
есть обобщенная гипергеометрическая функция pFq(αi, γi, z), содержащая р + q параметров. В частности, обобщенное Г. у. 3-го порядка, имеющее решение 3F2(α1, α2, α3, γ1, γ2, z), можно представить в форме
z2(1 - z)w''' + [1 + γ1 + γ2 - (3 + α1 + α2 + α3) z ] zw'' + [γ1γ2 - (1 + α1 + α2 + α3 + α1α2 + α2α3 + α3α1) z] w' - α1α2α3 w = 0.
Лит.: [l] Gauss C., «Comm. recentiores Soc. Göttingen», 1812, Bd 2; [2] Кратцер А., Франц В., Трансцендентные функции, пер. с нем., М., 1963; [3] Бейтмен Г., Эрдейи А., Высшие трансцендентные функции. Гипергеометрическая функция. Функции Лежандра, пер. с англ., 2 изд., М., 1973; [4] Камке Э., Справочник по обыкновенным дифференциальным уравнениям, пер. с нем., 5 изд., М., 1976; [5] Голубев В. В., Лекции по аналитической теории дифференциальных уравнений, 2 изд., М.-Л., 1950.
Н. Х. Розов.
Источники:
- Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'