ГИПЕРГЕОМЕТРИЧЕСКОЕ РАСПРЕДЕЛЕНИЕ

ГИПЕРГЕОМЕТРИЧЕСКОЕ РАСПРЕДЕЛЕНИЕ - распределение вероятностей, заданное формулой

(*)

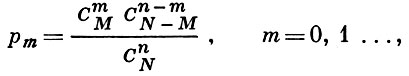
где М, N и n - целые неотрицательные числа и М ≤ N, n ≤ N (здесь С^b_a - биномиальный коэффициент). Г. р. обычно связано с выбором без возвращения, а именно: формула (*) указывает вероятность получения ровно m «отмеченных» элементов в случайной выборке объема n из генеральной совокупности, содержащей N элементов, среди к-рых М «отмеченных» и N - M «неотмеченных» элементов. При этом вероятность (*) определена лишь для

max(0, М + n - N) ≤ m ≤ min (n, М).

Однако определение (*) можно использовать при всех m ≥ 0, т. к. можно считать, что С^b_a = 0 при b > а, поэтому равенство Р_m = 0 нужно понимать как невозможность получить в выборке m «отмеченных» элементов. Сумма значений р_m, распространенная па все выборочное пространство, равна 1. Если обозначить M/N = p, то (*) можно переписать в иной форме:

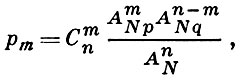
где

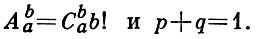
Если р постоянна и N → ∞, то имеет место биномиальное приближение

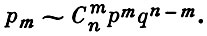
Среднее значение Г. р. не зависит от N и совпадает со средним пр. соответствующего биномиального распределения Дисперсия Г. р.

σ² = npq(N - n)/(N - 1)

не превосходит дисперсии биномиального закона σ² = npq. При N → ∞ моменты любого порядка Г. р. стремятся к соответствующим значениям моментов биномиального распределения. Производящая функция Г. р. имеет вид:

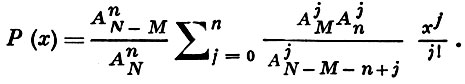
Ряд в правой части представляет собой гипергеометрическую функцию Р(α, β, γ, х), где α = -n, β = -M, γ = N - М - n + 1 (этому обстоятельству распределение обязано своим названием). Вероятность (*) и соответствующая функция распределения табулированы в широких пределах.

Лит.: [1] Lieberman G. I., Owen D. В., Tables of the Hypergeometric Probability Distribution, Stanford, 1961; [2] Оуэн Д. Б., Сборник статистических таблиц. Обработка таблиц, пер. с англ., М., 1966; [3] Большев Л. Н., Смирнов Н. В., Таблицы математической статистики, 2 изд М., 1968.

А. В. Прохоров.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.