ГИПЕРГЕОМЕТРИЧЕСКИЙ РЯД

ГИПЕРГЕОМЕТРИЧЕСКИЙ РЯД, ряд Гаусса - ряд вида

(*)

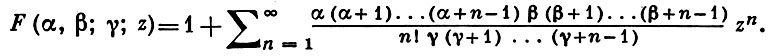
Г. р. имеет смысл, если γ не равно нулю или целому отрицательному числу; он сходится при |z| < 1. Если, кроме того, Re(γ - α - β) > 0, то Г. р. сходится и при z = 1. В этом случае справедлива формула Гаусса

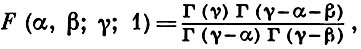
где Г(z) - гамма-функция. Аналитич. функция, определяемая с помощью Г. р., наз. гипергеометрической функцией.

Обобщенным гипергеометрическим рядом наз. ряд вида

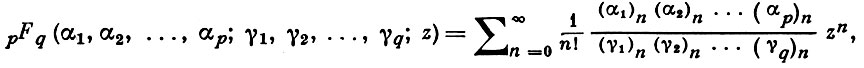
где (x)_n ≡ x(x + 1)...(x + n - 1). В этих обозначениях ряд (*) записывается как ₂F₁(α, β; γ; z).

Э. А. Чистова.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.